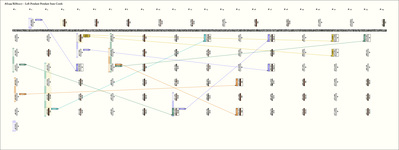
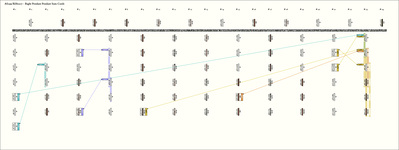
| Notes: |
Ascher Databook Notes:
- Construction note: The twisted end of the main cord was folded back and secured with a white cord wrapping.
- The khipu consists of 12 groups of pendants. Each group is united by a top cord. With the exception of the first group (which has one additional pendant), each has 6 pendant cords.
- Within groups 1, 4, and 11, all pendants and the top cord are the same color. Within groups 5, 6, 7, and 9, the first 3 pendants are one color, and the next 3 are another color. In 3 of these 4 groups, the top cord color differs from both the pendant colors. Within groups 8, 10, and 12, the first 3 pendants are one color and the next 3 are mixed. Within groups 2 and 3, the pendant colors are mixed. In 4 of these latter 5 groups, the top cord is one of the colors in the pendant group.
- Assuming that the broken 4th pendants in groups 3 and 11 have the values 37 and 433 respectively, the values on the top cords are the sums of the values in their associated groups. The exceptions are that the top cord value in group 11 is 1 less than the sum, and the value in group 4 is 2 more than its sum. Also, the first pendant in group 1 is an extra pendant in the group and so is not included in the sum.
- The sums of values in groups 1-4 in corresponding positions are found on pendants in later groups. Specifically:
\[ P_{8j}=\sum\limits_{i=1}^{4} P_{ij}\;\;\;for\;j=1 \]
\[ P_{11,j+1} = \sum\limits_{i=1}^{4} P_{ij}\;\;\;for\;j=4 \]
- However, when the pendant positions are read from left to right in some groups and from right to left in other groups, many more such sums are seen. Since our listing numbering is left to right, we denote that as the natural order (N) and, hence, right to left as the reverse order (R). The maximum number of relations are seen when the 12 groups are read with the following orders:
(R, N, N, R) (R, N, N, R) (N, R, N, R)
Parenthesis have been used to separate the orders of groups 1-4, groups 5-8, and groups 9-12; this is done in order to emphasize that when viewed as sets of 4 groups, there is some pattern to the ordering. Also, using this ordering, in the relations that follow, values from groups 1-4 and from groups 5-8 are often united.
- Sums of values in groups 1-4:
\[ P_{9,j+1}=\sum\limits_{i=1}^{4} P_{ij}\;\;\;for\;j=(2,4) \]
\[ P_{5,j+1}=\sum\limits_{i=1}^{4} P_{ij}\;\;\;for\;j=3 \]
\[ P_{11,j+1}=\sum\limits_{i=1}^{4} P_{ij}\;\;\;for\;j=5 \]
- Sums of values in groups 5-8:
\[ P_{3,j-2}=\sum\limits_{i=5}^{8} P_{ij}\;\;\;for\;j=5 \]
\[ \sum\limits_{i=5}^{8} P_{ij} = \sum\limits_{i=5}^{8} P_{i,j+3}\;\;\;for\;j=3 \]
P11,j = P5j + P8j = P6j + P9j for j=4
- Position by position, group 5 is the sum of groups 2 and 6:
P5j = P2j + P6j for j=(1,2,..., 6)
|