UR006/KH0242 - Pendant Pendant Sums
Drawings:
Right Handed Sums: # Sums = 12, Max # Summands = 19, (Min, Mean, Max) Sum Values = (11, 15, 21)
Click on Image to View Larger
Left Handed Sums: # Sums = 4, Max # Summands = 16, (Min, Mean, Max) Sum Values = (13, 17, 21)
Click on Image to View Larger
Right Handed Sum Detail: - Click on column name to sort
| # | Color | Sum Schema | Sum Cord | Sum Cord Value | # Summands | Summands |
|---|---|---|---|---|---|---|
| 1 |  | p416, 17 : 15KB | 15 | 2 | p65: 7GG:MB + p66: 8KB | |
| 2 |  | p628, 16 : 11MB | 11 | 8 | p66: 8KB + p67: 2MB:KB + p68: 0PK + p69: 0PK + p70: 0MB + p71: 0AB + p72: 0MB:KB + p73: 1MB | |
| 3 |  | p11213, 21 : 14AB:KB | 14 | 14 | p155: 3KB + p156: 1AB:KB + p157: 0PK + p158: 0MB + p159: 1AB + p160: 0MB + p161: 0MB + p162: 0MB + p163: 2AB + p164: 0MB + p165: 0MB + p166: 0MB + p167: 6AB + p168: 1MB | |
| 4 |  | p13015, 17 : 18MB | 18 | 19 | p133: 1MB + p134: 0AB:KB + p135: 0PK + p136: 0MB + p137: 0AB + p138: 0MB + p139: 1RB + p140: 0MB + p141: 1AB + p142: 0MB:KB + p143: 0MB + p144: 0MB + p145: 0AB + p146: 0MB:KB + p147: 3MB + p148: 1MB + p149: 3AB + p150: 0MB + p151: 8MB | |
| 5 |  | p19321, 14 : 12MB | 12 | 8 | p210: 2AB + p211: 0MB + p212: 3MB + p213: 0MB + p214: 1AB + p215: 1MB + p216: 4MB + p217: 1MB | |
| 6 |  | p20121, 22 : 19AB:GG | 19 | 15 | p223: 5KB + p224: 1AB:GG + p225: 0PK + p226: 0MB + p227: 2MB + p228: 0MB + p229: 2MB + p230: 0VR + p231: 1MB + p232: 0MB + p233: 1MB + p234: 3MB + p235: 0MB + p236: 3MB + p237: 1MB | |
| 7 |  | p22123, 19 : 21KB | 21 | 16 | p222: 2MB + p223: 5KB + p224: 1AB:GG + p225: 0PK + p226: 0MB + p227: 2MB + p228: 0MB + p229: 2MB + p230: 0VR + p231: 1MB + p232: 0MB + p233: 1MB + p234: 3MB + p235: 0MB + p236: 3MB + p237: 1MB | |
| 8 |  | p26827, 21 : 15MB | 15 | 6 | p275: 1VR + p276: 1MB + p277: 2MB + p278: 2MB + p279: 8MB + p280: 1MB | |
| 9 |  | p29129, 21 : 14AB:GG | 14 | 15 | p295: 2MB + p296: 0MB + p297: 1MB + p298: 0VR + p299: 0MB + p300: 0MB + p301: 0MB + p302: 3MB + p303: 0MB + p304: 2MB + p305: 0MB + p306: 3MB + p307: 0MB + p308: 2MB + p309: 1MB | |
| 10 |  | p31131, 19 : 16KB | 16 | 11 | p319: 1MB + p320: 0KB + p321: 0VR + p322: 2MB + p323: 0AB + p324: 0MB + p325: 1MB + p326: 1MB + p327: 4AB + p328: 0MB + p329: 7KB | |
| 11 |  | p33433, 19 : 11KB | 11 | 2 | p340: 1KB + p341: 10MB | |
| 12 |  | p36237, 19 : 11KB | 11 | 12 | p365: 5AB:GG + p366: 0PK + p367: 0VR + p368: 0MB + p369: 1MB + p370: 0MB + p371: 1MB + p372: 0VR + p373: 0MB + p374: 1MB + p375: 1MB + p376: 2MB |
Left Handed Sum Detail: - Click on column name to sort
| # | Color | Sum Schema | Sum Cord | Sum Cord Value | # Summands | Summands |
|---|---|---|---|---|---|---|
| 1 | 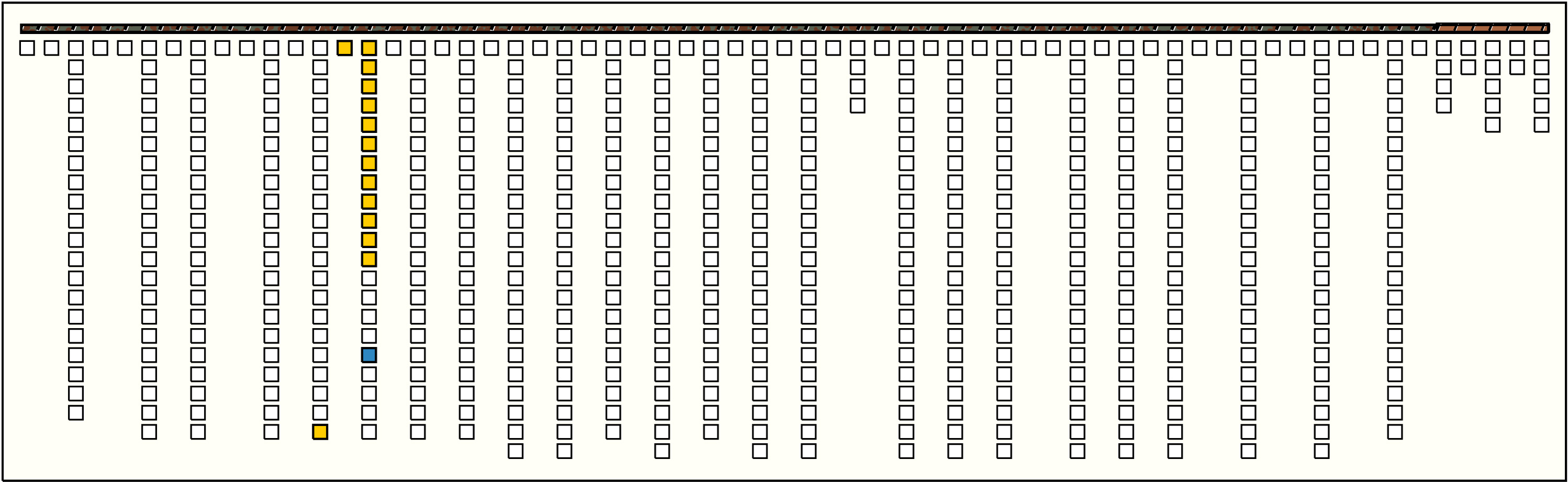 | p13015, 17 : 18MB | 18 | 14 | p112: 14AB:KB + p113: 0PK + p114: 0MB + p115: 0AB + p116: 0AB:KB + p117: 0MB + p118: 0MB + p119: 0AB + p120: 0MB:KB + p121: 1MB + p122: 0MB + p123: 0AB + p124: 0AB:MB + p125: 3MB | |
| 2 | 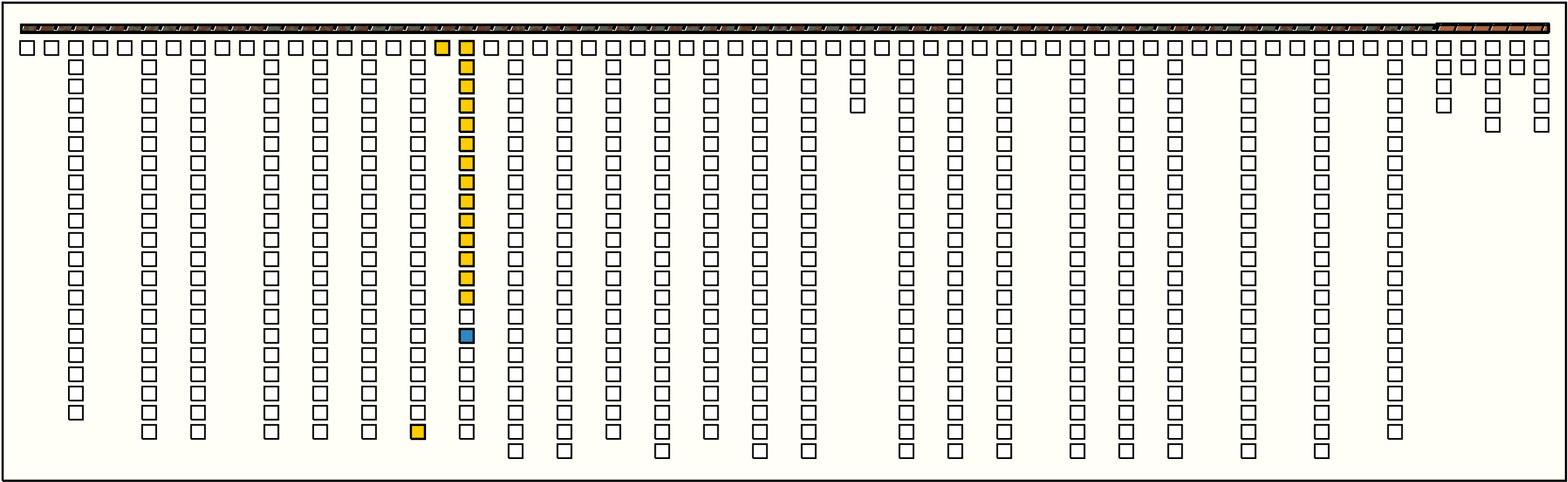 | p17319, 16 : 13MB | 13 | 16 | p156: 1AB:KB + p157: 0PK + p158: 0MB + p159: 1AB + p160: 0MB + p161: 0MB + p162: 0MB + p163: 2AB + p164: 0MB + p165: 0MB + p166: 0MB + p167: 6AB + p168: 1MB + p169: 1MB + p170: 0MB + p171: 1AB | |
| 3 | 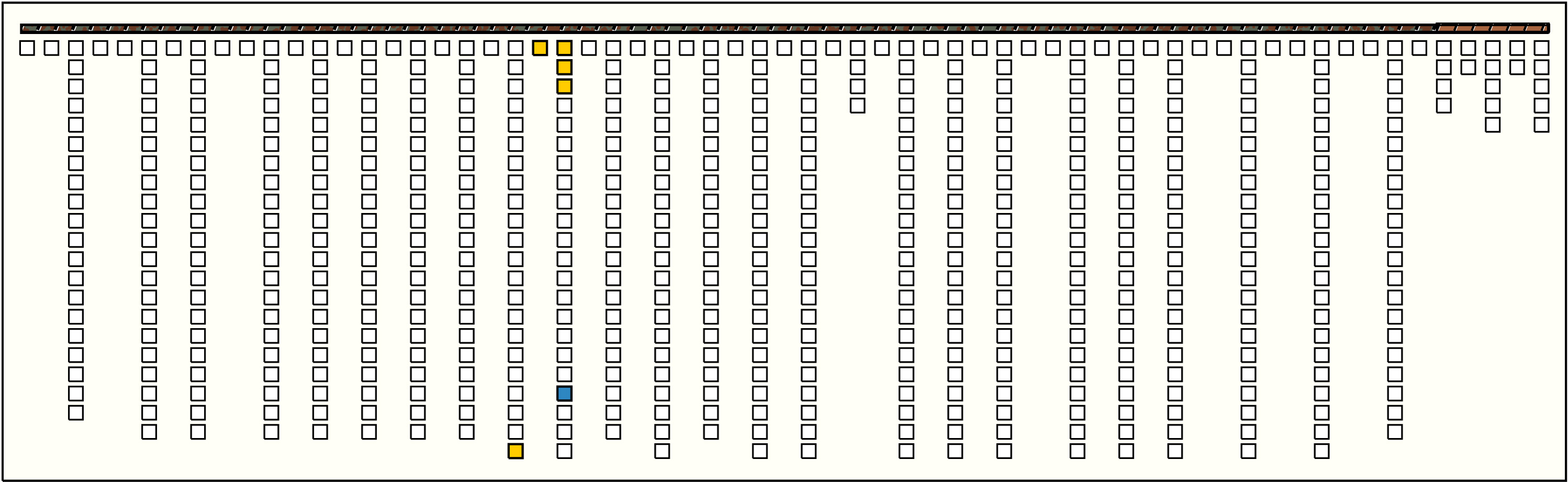 | p22123, 19 : 21KB | 21 | 5 | p201: 19AB:GG + p202: 0PK + p203: 0VR + p204: 0MB + p205: 2MB | |
| 4 |  | p31131, 19 : 16KB | 16 | 5 | p291: 14AB:GG + p292: 0PK + p293: 0VR + p294: 0MB + p295: 2MB |
Khipu Notes:
Fieldguide Notes:

Top Pendant

Loop Pendant
Notes excerpted from Gary Urton (2001). A Calendrical and Demographic Tomb Text from Northern Peru. Latin American Antiquity, 12(2), 127–147. doi:10.2307/972052
Before proceeding, I should note that in the calendrical analysis of khipu UR006 that I will present in this section, I will disregard the 32 pendant strings on this sample that do not conform to the regular arrangement of paired-that is: [20, 21, 22] + [8, 9, 10] sets of pendant strings as outlined above. The excluded pendant strings are Clusters #59-#63 at the right end of the primary cord - AMK. The knot counts on these excluded strings will come into play later in my analysis. I believe that these strings, which do not conform to the pattern of paired sets, may have been used, in some manner that I do not entirely understand at present, to provide flexibility in relation to one of the principal uses of this khipu-that is, as a biennial calendar.
There are two clear indications of the calendrical significance of the organization of pendants strings on khipu UR006. The first indication is the number of strings in each of the paired sets; that is, if we take the mean value of the number of pendant strings in the 24 paired sets, we arrive at a (theoretical) repetitive combination of 2 1 + 9 ( = 30) pendant strings (see Figure 5). This count is, of course, the whole number value closest to the number of days in a synodic lunar month (= 29.53 days). If each one of the 24 paired sets in khipu UR006 contained the mean number strings (i.e., 2 1 + 9 = 30), this would produce total of 720 pendant strings (30 x 24 = 720). One-half of this total would give us 360 pendant strings, a number which is close to an annual calendar count of 365 days. However, when we count the actual numbers of pendant and loop pendant strings in the 24 paired sets (see Figure 7), we arrive at the number 730; one-half of this total count is 365, a number that coincides with the number of days in what is known as the "vague year" (i.e., the whole number of days in a solar year of 365.242 days). Thus, khipu UR006 appears on a superficial look to represent a calendar integrating 24 essentially synodic lunar periods into two (vague) year counts. The respective pendant string counts for these four half-year periods are illustrated in Figure 8 and summarized in schematic form in Table 1. In Figure 8 and Table 1, we note that the 12 paired sets of pendant and loop pendant strings in Year One contain a total count of 362; the 12 paired sets for Year Two contain a count of 368 strings. Thus, the average count of what I am calling herein the two years recorded in khipu UR006 is 365 (i.e., 362 + 368 = 730 7 2 = 365).
It is interesting to note what in fact emerges if we divide each of the two groupings of 12 paired sets of pendant strings in half, thereby producing what should, according to the calendrical interpretation offered here, represent four half-year periods (see especially Table 1). As we note in Table 1, the halfyear labeled Year One (a) contains 179 pendant strings and the half-year labeled Year Two ( c) contains 185 pendants. Now 179 is one-half day more than the count of the number of days covered by the perihelion; this is the period of time of the sun's (apparent) movement from the September equinox through the December solstice and back to the March equinox. The number 185 is one and one-half days less than the count of the number of days covered by the aphelion, which is the period of the sun's (apparent) from the March equinox through the solstice and back to the September equinox. Thus, although such an interpretation result in a biennial calendar of discontinuous, quarterly (i.e., four half-year), nonetheless, given the sums of pendant contained in the half-years la and 2c, we allow for the possibility that the biennial calendar khipu UR006 was reckoned in the pairings: 1a + 2c (=364) and 1b + 2d (=366), rather than of the : 1a + 1b (=362) and 2c + 2d (=368).
The main point to appreciate with respect to this discussion is that khipu UR006 appears to represent a calendar count. We should pause for a moment to consider the rather unusual circumstance of finding a khipu recording a double, rather than a single, year count. It is relevant to note in this regard that the Inkas exhibited a strong emphasis on pairing and dualism in many aspects of their material culture and sociopolitical organization. For instance, in terms of material culture, Cummins has shown convincingly in his studies of Inka keros, the Inka ceremonial drinking cups, that these vessels were always produced in pairs.
Although we do not have extensive documentation for an equal emphasis on dualism among the preInkaic Chachapoya, there are certain data that do support the importance of this organizational principle in this region and in its material culture as well. For instance, we find a notable emphasis on paired artifacts in the material recovered from the chullpas at Laguna de los Cóndores. There are several pairs of pyro-engraved drinking gourds, each pair of which is decorated with virtually identical designs, found among the grave goods. I would note the very interesting ethnographic datum reported by Schjellerup in which she reports that, prior to 1960, villages in the region were paired for the purposes of maintaining the road system, the bridges, and the canals. This information is particularly interesting in relation to the interpretation I will develop below regarding the two-year calendar of khipu UR006 as a record of labor service in the region in the late prehispanic period. Finally, Lerche detects not only a strong dualistic organizational principle in Chachapoya sociopolitical organization, but he also argues that when polities in the past were divided into dual groupings--one example of which is the dualism Chilcho/Llaja"-these entities were each further subdivided into nine subdivisions (Lerche 1995:58--6 1). Thus, whether the calendrical khipu under consideration (i.e., UR006) was manufactured used by the pre-lnkaic Chachapoyans or by the administrators after their entry into Chachapoya, we ought not, in fact, be surprised to find the calendar specialist(s) constructed a two-year calendar count.
Therefore, at this first level of analysis, we can conclude that one of the messages the people from Laqtacocha (or elsewhere) would have been reminded of when they visited the tombs at Laguna de los Cóndores and took up khipu UR006 was a powerful representation of what I would term the ideal, or proper, structure and organization of time-i.e., as a unit composed of two complementary, probably interconnected vague year counts.
As we will see below, the above interpretation has only scratched the surface of the calendrical information encoded in khipu VR6. However, in order to understand the additional temporal information that was encoded into the strings of khipu VR6, we must shift our attention to the knot counts that are containedon the pendant and loop pendant strings of this khipu. In the course of this analysis, we will identify another possible use of this knotted-string record that is an account of the organization of tributepayers in the region of Laguna de los Cóndores in late prehispanic times.
This khipu also displays remarkably close approximations of multiple solar-year counts (= S in Table 2). These are seen in the periods of: a) 1, 826, which is two-tenths of a day less than five solar years, and b) 730, which is one-half of a day less than two solar years. What is perhaps most striking about the calendrical periodicities encoded into khipu UR006 are those cases in which there are correlations of different lunar cycles with the solar year count(s). For example, the total knot count on the pendants and loop pendants of Year Two (= 977) is two and onehalf days more than 33 synodic lunar months and/or six-tenths of a day more than two solar years plus nine sidereal lunar cycles. One sees a similar correlation of a lunar (sidereal) periodicity and the solar year count in the knot count on pendant strings in Year Two (= 446; see Table 2 for the calendrical correlation).
The organization of knot values tied into the pendants and loop pendants of this khipu sample provide the information for very complex and sophisticated calendrical reckoning and correlations. The calendrical interpretation of khipu UR006 presented here should be considered provisional. As further studies of additional khipu samples from Laguna de los Cóndores are completed, and as these studies are brought into relationship with studies of the historical documents from the region, it is hoped that we will arrive at fuller and more contextualized views how and why certain astronomical observations were made, and calendrical calculations and correlations were performed,by the Chachapoya-Inka khipukamayuqs.
In the Inka decimal administrative organization, the principal accounting units among the (as elsewhere throughout the empire; see Julien 1988 and Murra 1982) were groupings of chanka ("10"), pachaqa ("100"), waranqa ("1000"), and hunu ("10,000") tribute- payers. Subjects of the were required to pay tribute within these decimal of accounting. As is well-known, in the empire, the manner of "paying tribute" was the performance of labor service for the . This was undertaken in mit 'a, "turns" of labor performed by different tributary groups working succession (see Murra 1982). Now, we learn one document, which dates to 1572, that during times, the cacique principal (the top political administrative official) of the large region just to the south and west of de los Cóndores was a man named Guaman (who is described in this document as the "lord" senor) of the three waranqas (=3000 tribute payers) Cajamarquilla, Condormarca, and Bambamarca.
Soon after the Spanish entered the Chachapoya region, in 1535, Alonso de Alvarado was awarded encomienda of Cochabamba, Leymebamba, and this grant included the ayllus of Chilchos who were removed to colonial reducciones towns") from the area around Laguna de los Cóndores. is critical to note is that, at the time of establishment of this encomienda grant, Alvarado said to have taken census information from a local named Francisco Pizarro Guaman. As we learn reading the colonial documents from this region, Francisco Pizarro Guaman was the same man identified earlier (i.e., in the document from 1572; see above) as "Guaman," the ChachapoyaInka ;ue principal of the 3,000 tribute-payers in this region. Francisco Guaman is said to have provided Alvarado with census data from khipu accounts his (Guaman's) possession. In that census account, made in 1535, the total number of tribute-payers, or mit'a laborers, was given as three waranqas-i.e., 3,000 see Schjellerup 1997:40, 318).
The number 3,000, or three waranqas, may have been a rounded-off, or "idealized," number, as we often find in colonial documentation pertaining to censuses and tribute records. Nonetheless, I find it remarkable and quite suggestive how closely the initial census count of 3,000 mit'a laborers approximates the values encoded into the biennial calendar count in khipu VR6 from Laguna de los Cóndores.
To recapitulate, when we subtract the knot values tied into the circled pendant groups within each of the two "year counts" that do not conform to the calendrical organization in khipu VR6, we arrive at the total of 3,005 (= 2,028 + 977). I hypothesize that this value, and therefore khipu VR6 itself, referred to the total number of tribute-payers in the region of Laguna de los Cóndores, Leymebamba, and Cochabamba in late prehispanic (i.e., ChachapoyaInka) times.
Although it is hoped that the interpretation offered above in the form of a hypothesis has at least gone some distance toward explaining how and why khipu UR006 was constructed as it is, it is also clearly recognized by the author that there are, in fact, many more new questions raised by this interpretation. questions include the following: If khipu UR006, indeed, a biennial tributary record, then where the first year begin? At the top or at the bottom the khipu? At what point in the annual cycle does calendar begin ( e.g., at one or the other of the ? At one or the other of the equinoxes?)?, if this is a two-year calendar of state service was performed by people in this region, does the show that twice as many people worked in One as in Year Two? And finally, why were there great differences in the numbers of tributaries worked for the state from one month to the next? cannot provide convincing answers to any of these at the present time. However, we are at least asking questions of khipu records that have been asked before, and hopefully some of these can help guide our future investigations of knotted-string records in productive directions in creative ways.
Finally, and as a corollary to the hypothesis articulated above with regard to the integrated nature of calendrical and demographic information into khipu UR006, I would further hypothesize this khipu may have been the actual accounting from which Lord (Francisco Pizarro) supplied census figures to Alonso de, in 1535. This latter hypothesis implies that mummified remains of Francisco Pizarro Guaman be among the 220 or so mummy bundles from Laguna de los Cóndores.
When descendants of the mallki( s) at Laguna de los Cóndores visited the ancestor-custodian of khipu UR006, they could have taken up the khipu in order to themselves of the proper, or "standard," organization of time and the calendar, as well as the appropriate," traditional division and organization labor service to the state performed in the past by populace in the region. During precolumbian, these "messages from the mallkis" would have of contemporary relevance, as a record of their labor service obligation to the Inka state. the Spanish conquest, the accounting of time sociopolitical organization contained in khipu 6 would have served the people of the region as historical document against which to measure and certain changes that had occurred in their since the beginning of Spanish domination in region. As in the reading of all texts, the reading the information encoded into khipu UR006 would have been subject to the (re-)interpretations of each reader, as well as each generation of readers. new reading of the tomb text, whether its was the same as or different from the last, would have been sanctioned by the presence of the mallki.

Top Pendant

Loop Pendant

Notes excerpted from Gary Urton (2001). A Calendrical and Demographic Tomb Text from Northern Peru. Latin American Antiquity, 12(2), 127–147. doi:10.2307/972052
The Organization of Calendrical Information in Khipu UR006
Khipu UR006 contains a total of 762 pendant strings made of Z-spun, S-ply cotton fibers. Compared to other khipus in this collection, the pendant strings of khipu UR006 are attached to the primary cord and organized in an unusual, highly systematic manner. That is, with only a few exceptions, the basic unit of organization of the pendant strings is a paired set. One member of these paired sets is composed of either 20, 21, or 22 pendant strings; these pendant strings are attached directly to the primary cord. The other member of each paired set is composed of 8, 9, or 10 pendant strings. These latter pendants, however, are not attached directly to the primary cord; rather, they are attached to a string whose two ends are themselves attached to the primary cord. These "intermediary" strings (i.e., as they stand between, and connect, the pendant strings and the primary cord) hang down below the primary cord in a slight arc, or loop. I will refer to these intermediary strings and the pendants attached to them as "loop pendants." There are 24 groups of these paired sets of pendant strings and loop pendants on khipu UR006 (see Figures 6 and 7). Note by Ashok Khosla. The small loop pendant set of {8,9,10} cords are labeled as top cords in the Harvard KDB, and as such, are drawn here as top cords.Before proceeding, I should note that in the calendrical analysis of khipu UR006 that I will present in this section, I will disregard the 32 pendant strings on this sample that do not conform to the regular arrangement of paired-that is: [20, 21, 22] + [8, 9, 10] sets of pendant strings as outlined above. The excluded pendant strings are Clusters #59-#63 at the right end of the primary cord - AMK. The knot counts on these excluded strings will come into play later in my analysis. I believe that these strings, which do not conform to the pattern of paired sets, may have been used, in some manner that I do not entirely understand at present, to provide flexibility in relation to one of the principal uses of this khipu-that is, as a biennial calendar.
There are two clear indications of the calendrical significance of the organization of pendants strings on khipu UR006. The first indication is the number of strings in each of the paired sets; that is, if we take the mean value of the number of pendant strings in the 24 paired sets, we arrive at a (theoretical) repetitive combination of 2 1 + 9 ( = 30) pendant strings (see Figure 5). This count is, of course, the whole number value closest to the number of days in a synodic lunar month (= 29.53 days). If each one of the 24 paired sets in khipu UR006 contained the mean number strings (i.e., 2 1 + 9 = 30), this would produce total of 720 pendant strings (30 x 24 = 720). One-half of this total would give us 360 pendant strings, a number which is close to an annual calendar count of 365 days. However, when we count the actual numbers of pendant and loop pendant strings in the 24 paired sets (see Figure 7), we arrive at the number 730; one-half of this total count is 365, a number that coincides with the number of days in what is known as the "vague year" (i.e., the whole number of days in a solar year of 365.242 days). Thus, khipu UR006 appears on a superficial look to represent a calendar integrating 24 essentially synodic lunar periods into two (vague) year counts. The respective pendant string counts for these four half-year periods are illustrated in Figure 8 and summarized in schematic form in Table 1. In Figure 8 and Table 1, we note that the 12 paired sets of pendant and loop pendant strings in Year One contain a total count of 362; the 12 paired sets for Year Two contain a count of 368 strings. Thus, the average count of what I am calling herein the two years recorded in khipu UR006 is 365 (i.e., 362 + 368 = 730 7 2 = 365).
It is interesting to note what in fact emerges if we divide each of the two groupings of 12 paired sets of pendant strings in half, thereby producing what should, according to the calendrical interpretation offered here, represent four half-year periods (see especially Table 1). As we note in Table 1, the halfyear labeled Year One (a) contains 179 pendant strings and the half-year labeled Year Two ( c) contains 185 pendants. Now 179 is one-half day more than the count of the number of days covered by the perihelion; this is the period of time of the sun's (apparent) movement from the September equinox through the December solstice and back to the March equinox. The number 185 is one and one-half days less than the count of the number of days covered by the aphelion, which is the period of the sun's (apparent) from the March equinox through the solstice and back to the September equinox. Thus, although such an interpretation result in a biennial calendar of discontinuous, quarterly (i.e., four half-year), nonetheless, given the sums of pendant contained in the half-years la and 2c, we allow for the possibility that the biennial calendar khipu UR006 was reckoned in the pairings: 1a + 2c (=364) and 1b + 2d (=366), rather than of the : 1a + 1b (=362) and 2c + 2d (=368).
The main point to appreciate with respect to this discussion is that khipu UR006 appears to represent a calendar count. We should pause for a moment to consider the rather unusual circumstance of finding a khipu recording a double, rather than a single, year count. It is relevant to note in this regard that the Inkas exhibited a strong emphasis on pairing and dualism in many aspects of their material culture and sociopolitical organization. For instance, in terms of material culture, Cummins has shown convincingly in his studies of Inka keros, the Inka ceremonial drinking cups, that these vessels were always produced in pairs.
Although we do not have extensive documentation for an equal emphasis on dualism among the preInkaic Chachapoya, there are certain data that do support the importance of this organizational principle in this region and in its material culture as well. For instance, we find a notable emphasis on paired artifacts in the material recovered from the chullpas at Laguna de los Cóndores. There are several pairs of pyro-engraved drinking gourds, each pair of which is decorated with virtually identical designs, found among the grave goods. I would note the very interesting ethnographic datum reported by Schjellerup in which she reports that, prior to 1960, villages in the region were paired for the purposes of maintaining the road system, the bridges, and the canals. This information is particularly interesting in relation to the interpretation I will develop below regarding the two-year calendar of khipu UR006 as a record of labor service in the region in the late prehispanic period. Finally, Lerche detects not only a strong dualistic organizational principle in Chachapoya sociopolitical organization, but he also argues that when polities in the past were divided into dual groupings--one example of which is the dualism Chilcho/Llaja"-these entities were each further subdivided into nine subdivisions (Lerche 1995:58--6 1). Thus, whether the calendrical khipu under consideration (i.e., UR006) was manufactured used by the pre-lnkaic Chachapoyans or by the administrators after their entry into Chachapoya, we ought not, in fact, be surprised to find the calendar specialist(s) constructed a two-year calendar count.
Therefore, at this first level of analysis, we can conclude that one of the messages the people from Laqtacocha (or elsewhere) would have been reminded of when they visited the tombs at Laguna de los Cóndores and took up khipu UR006 was a powerful representation of what I would term the ideal, or proper, structure and organization of time-i.e., as a unit composed of two complementary, probably interconnected vague year counts.
As we will see below, the above interpretation has only scratched the surface of the calendrical information encoded in khipu VR6. However, in order to understand the additional temporal information that was encoded into the strings of khipu VR6, we must shift our attention to the knot counts that are containedon the pendant and loop pendant strings of this khipu. In the course of this analysis, we will identify another possible use of this knotted-string record that is an account of the organization of tributepayers in the region of Laguna de los Cóndores in late prehispanic times.
The Significance of Knot Values in khipu UR006
As is well-known, many (but by no means all/ khipus incorporated a hierarchical decimal organization in the arrangement of knots tied into pendant strings such that there were different types of knots tied inclusters on different levels along the length of the pendant strings as place-value indicators of 1s, 10s, 100s, 1,000s, and 10,000s (see Ascher and Ascher 1997 [ 198 1]; Garcilaso de la Vega 1966: 330-33 1 [ 1609- 17]; Locke 1923; Urton 1994). In Figure 9, I provide a reading of the numerical values of the knots tied into the pendant and loop pendant strings of khipu UR006. In terms of the construction of knots in this sample, I would note that the majority of knots in khipu UR006 are tied as, what I have termed in an earlier study (see Urton 1994), Z-knots. However, there are also several scattered examples of S-knots on this 10 sample (see below). In the interpretation of knot-count values presented in Figure 9, I have divided the khipu at the following places: a) the non-paired groupings of estrings at the bottom of the khipu are set off from the pendants and loop pendants composing what was interpreted above as the biennial calendar count; b) another division is made between the two annual periods of the biennial calendar count; and c) subdivisions of the two yearly counts are made (as in Figure 8 and Table 1) to produce four half-year periods. I will first consider the calendrical information encoded in the knot counts illustrated in Figure 9.The Calendrical Information in the Knot Values of Khipu UR006
When we study carefully the knot values tied into the pendant and loop pendant strings of khipu UR006, we encounter a rather stunning amount of calendrical information (Table 2). We are aware from earlier studies of Inka calendrics (see especially Zuidema 1977 and 1989) that Inka calendar specialists had a particular interest in observing both the sidereal lunar cycle as well as the synodic lunar cycle, and in correlating these lunar periodicities with the solar year of 365.242 days. These calendrical periodicities, and the apparent interest in correlating them, are also evident in the Chachapoya-Inka calendar in khipu UR006. For example, we find in the knot values of khipu UR006 that the calendar specialists in Chachapoyas had recorded numbers that were very close numerical equivalents of sets of sidereal lunar cycles (= L1 in Table 2) composed of groupings of . 1 10 (-0.4 day), 1 12 (- 1. 1 days), and 1 13 (-2.3 days) sidereal lunar cycles; these values are encoded in khipu UR006 by the values (respectively) of 3,005, 3,059, and 3,085.This khipu also displays remarkably close approximations of multiple solar-year counts (= S in Table 2). These are seen in the periods of: a) 1, 826, which is two-tenths of a day less than five solar years, and b) 730, which is one-half of a day less than two solar years. What is perhaps most striking about the calendrical periodicities encoded into khipu UR006 are those cases in which there are correlations of different lunar cycles with the solar year count(s). For example, the total knot count on the pendants and loop pendants of Year Two (= 977) is two and onehalf days more than 33 synodic lunar months and/or six-tenths of a day more than two solar years plus nine sidereal lunar cycles. One sees a similar correlation of a lunar (sidereal) periodicity and the solar year count in the knot count on pendant strings in Year Two (= 446; see Table 2 for the calendrical correlation).
The organization of knot values tied into the pendants and loop pendants of this khipu sample provide the information for very complex and sophisticated calendrical reckoning and correlations. The calendrical interpretation of khipu UR006 presented here should be considered provisional. As further studies of additional khipu samples from Laguna de los Cóndores are completed, and as these studies are brought into relationship with studies of the historical documents from the region, it is hoped that we will arrive at fuller and more contextualized views how and why certain astronomical observations were made, and calendrical calculations and correlations were performed,by the Chachapoya-Inka khipukamayuqs.
Khipu and Documentary Accounts of TributePayers around Laguna de los Cóndores
The other type of information that it appears likely the khipukamayuqs of the southern Chachapoya region encoded into khipu UR006 is an accounting of tribute-payers that belonged to the ayllus or pachaqas in this region. This information is included primarily the knot values of khipu UR006. That is, as we see in the knot counts (i .e., the decimal values) presented in Figure 9, the knot count for Year One totals 2,059 (i.e., 2,028 + 3 1 = 2,059), while the Year Two -count totals exactly 1,000 (i.e., 977 + 23 = 1,000). These two values give a total (biennial) knot of 3,059. However, if we eliminate the three of pendant strings circled in Figure 9 (i.e., 3 1 23 = 54), which are those string groups not organized according to the pairing of pendant and loop pendant strings within the two-year counts, we end with a total, biennial knot count of 3,005. As we see below, this knot count is very close to the number of tribute-payers that were counted in first census of the population (i.e ., the descendants the mallkis at Laguna de los Cóndores) made in this region in early colonial times.In the Inka decimal administrative organization, the principal accounting units among the (as elsewhere throughout the empire; see Julien 1988 and Murra 1982) were groupings of chanka ("10"), pachaqa ("100"), waranqa ("1000"), and hunu ("10,000") tribute- payers. Subjects of the were required to pay tribute within these decimal of accounting. As is well-known, in the empire, the manner of "paying tribute" was the performance of labor service for the . This was undertaken in mit 'a, "turns" of labor performed by different tributary groups working succession (see Murra 1982). Now, we learn one document, which dates to 1572, that during times, the cacique principal (the top political administrative official) of the large region just to the south and west of de los Cóndores was a man named Guaman (who is described in this document as the "lord" senor) of the three waranqas (=3000 tribute payers) Cajamarquilla, Condormarca, and Bambamarca.
Soon after the Spanish entered the Chachapoya region, in 1535, Alonso de Alvarado was awarded encomienda of Cochabamba, Leymebamba, and this grant included the ayllus of Chilchos who were removed to colonial reducciones towns") from the area around Laguna de los Cóndores. is critical to note is that, at the time of establishment of this encomienda grant, Alvarado said to have taken census information from a local named Francisco Pizarro Guaman. As we learn reading the colonial documents from this region, Francisco Pizarro Guaman was the same man identified earlier (i.e., in the document from 1572; see above) as "Guaman," the ChachapoyaInka ;ue principal of the 3,000 tribute-payers in this region. Francisco Guaman is said to have provided Alvarado with census data from khipu accounts his (Guaman's) possession. In that census account, made in 1535, the total number of tribute-payers, or mit'a laborers, was given as three waranqas-i.e., 3,000 see Schjellerup 1997:40, 318).
The number 3,000, or three waranqas, may have been a rounded-off, or "idealized," number, as we often find in colonial documentation pertaining to censuses and tribute records. Nonetheless, I find it remarkable and quite suggestive how closely the initial census count of 3,000 mit'a laborers approximates the values encoded into the biennial calendar count in khipu VR6 from Laguna de los Cóndores.
To recapitulate, when we subtract the knot values tied into the circled pendant groups within each of the two "year counts" that do not conform to the calendrical organization in khipu VR6, we arrive at the total of 3,005 (= 2,028 + 977). I hypothesize that this value, and therefore khipu VR6 itself, referred to the total number of tribute-payers in the region of Laguna de los Cóndores, Leymebamba, and Cochabamba in late prehispanic (i.e., ChachapoyaInka) times.
Conclusions and Questions for Future Studies
The important point to stress from the analyses given above is the coincidence between what I have interpreted as a) calendrical values, and b) census figures (for tribute-payers) on khipu VR6. The crux of my argument is that this was, in fact, a coincidence of numerical value-that is, they were complementary, not contradictory. What I mean by this is that the calendrical of (Francisco Pizarro) Guaman's khipu would have provided the temporal pattern for the organization of mit ' a labor service provided to the Inka state in the region prior to the Spanish conquest. The knot count pertaining to each paired set of pendant and loop pendant strings would indicated the number of tribute payers that would have been responsible for performing state labor service in the region during one synodic lunar over the two-year accounting period encoded the strings and knots of khipu VR6.Although it is hoped that the interpretation offered above in the form of a hypothesis has at least gone some distance toward explaining how and why khipu UR006 was constructed as it is, it is also clearly recognized by the author that there are, in fact, many more new questions raised by this interpretation. questions include the following: If khipu UR006, indeed, a biennial tributary record, then where the first year begin? At the top or at the bottom the khipu? At what point in the annual cycle does calendar begin ( e.g., at one or the other of the ? At one or the other of the equinoxes?)?, if this is a two-year calendar of state service was performed by people in this region, does the show that twice as many people worked in One as in Year Two? And finally, why were there great differences in the numbers of tributaries worked for the state from one month to the next? cannot provide convincing answers to any of these at the present time. However, we are at least asking questions of khipu records that have been asked before, and hopefully some of these can help guide our future investigations of knotted-string records in productive directions in creative ways.
Finally, and as a corollary to the hypothesis articulated above with regard to the integrated nature of calendrical and demographic information into khipu UR006, I would further hypothesize this khipu may have been the actual accounting from which Lord (Francisco Pizarro) supplied census figures to Alonso de, in 1535. This latter hypothesis implies that mummified remains of Francisco Pizarro Guaman be among the 220 or so mummy bundles from Laguna de los Cóndores.
When descendants of the mallki( s) at Laguna de los Cóndores visited the ancestor-custodian of khipu UR006, they could have taken up the khipu in order to themselves of the proper, or "standard," organization of time and the calendar, as well as the appropriate," traditional division and organization labor service to the state performed in the past by populace in the region. During precolumbian, these "messages from the mallkis" would have of contemporary relevance, as a record of their labor service obligation to the Inka state. the Spanish conquest, the accounting of time sociopolitical organization contained in khipu 6 would have served the people of the region as historical document against which to measure and certain changes that had occurred in their since the beginning of Spanish domination in region. As in the reading of all texts, the reading the information encoded into khipu UR006 would have been subject to the (re-)interpretations of each reader, as well as each generation of readers. new reading of the tomb text, whether its was the same as or different from the last, would have been sanctioned by the presence of the mallki.

