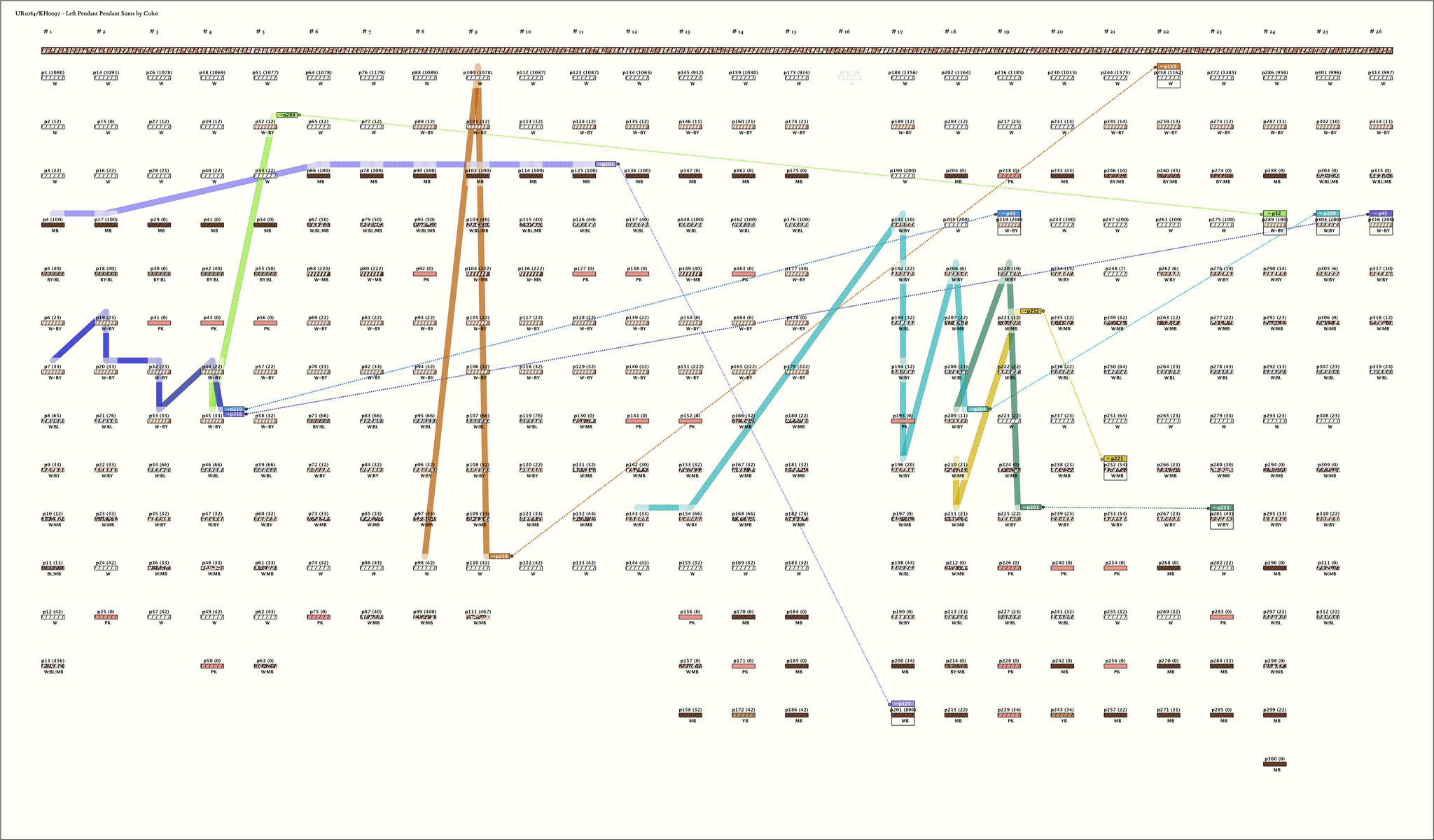
UR1084/KH0097 - Colored Pendant Sums

Drawings:

Overview	Detail View
All Khipus' Ascher Sum Fieldmarks	Right-Handed XRay
All Colored Pendant Sum Relationships	Left-Handed XRay
This Khipu's Fieldmark Catalog	Right-Handed Sum Detail
This Khipu's Drawing	Left-Handed Sum Detail

Right Handed Sums: # Sums = 4, Max # Summands = 4, (Min, Mean, Max) Sum Values = (66, 74, 76)
Click on Image to View Larger

Left Handed Sums: # Sums = 8, Max # Summands = 8, (Min, Mean, Max) Sum Values = (43, 345, 1162)
Click on Image to View Larger

Right Handed Sum Detail: - Click on column name to sort

#	Sum Cord	Sum Cord Value	# Summands	Summands
1	p21_{2, 8} : 76_W:BL	76	3	p213: 31_W:BL + p222: 22_W:BL + p227: 23_W:BL
2	p119_{10, 8} : 76_W:BL	76	3	p213: 31_W:BL + p222: 22_W:BL + p227: 23_W:BL
3	p168_{14, 10} : 66_W:MB	66	4	p210: 21_W:MB + p211: 21_W:MB + p221: 12_W:MB + p235: 12_W:MB
4	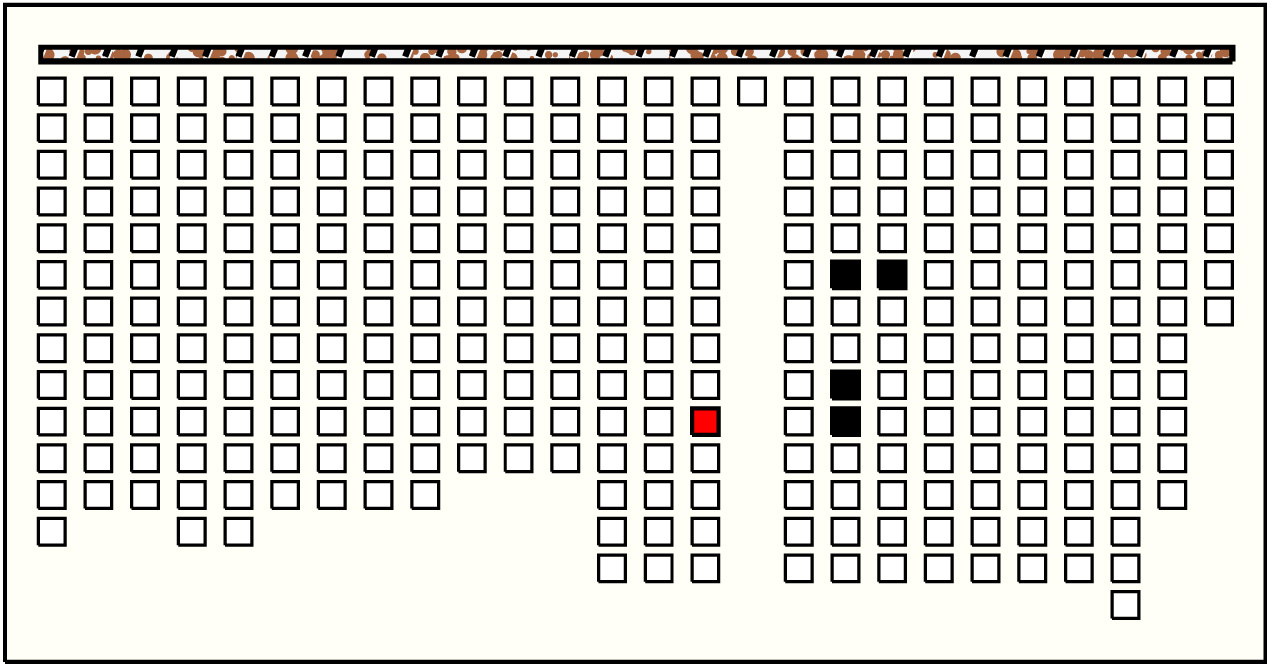p182_{15, 10} : 76_W:MB	76	4	p207: 22_W:MB + p210: 21_W:MB + p211: 21_W:MB + p221: 12_W:MB

Left Handed Sum Detail: - Click on column name to sort

#	Sum Cord	Sum Cord Value	# Summands	Summands
1	p201_{17, 14} : 800_MB	800	8	p4: 100_MB + p17: 100_MB + p66: 100_MB + p78: 100_MB + p90: 100_MB + p102: 100_MB + p114: 100_MB + p125: 100_MB
2	p219_{19, 4} : 200_W-BY	200	7	p7: 33_W-BY + p19: 23_W-BY + p20: 33_W-BY + p32: 23_W-BY + p33: 33_W-BY + p44: 22_W-BY + p45: 33_W-BY
3	p252_{21, 9} : 54_W:MB	54	3	p210: 21_W:MB + p211: 21_W:MB + p221: 12_W:MB
4	p258_{22, 1} : 1162_W	1162	3	p98: 42_W + p100: 1078_W + p110: 42_W
5	p281_{23, 10} : 43_W:BY	43	3	p209: 11_W:BY + p220: 10_W:BY + p225: 22_W:BY
6	p289_{24, 4} : 100_W-BY	100	4	p33: 33_W-BY + p44: 22_W-BY + p45: 33_W-BY + p52: 12_W-BY
7	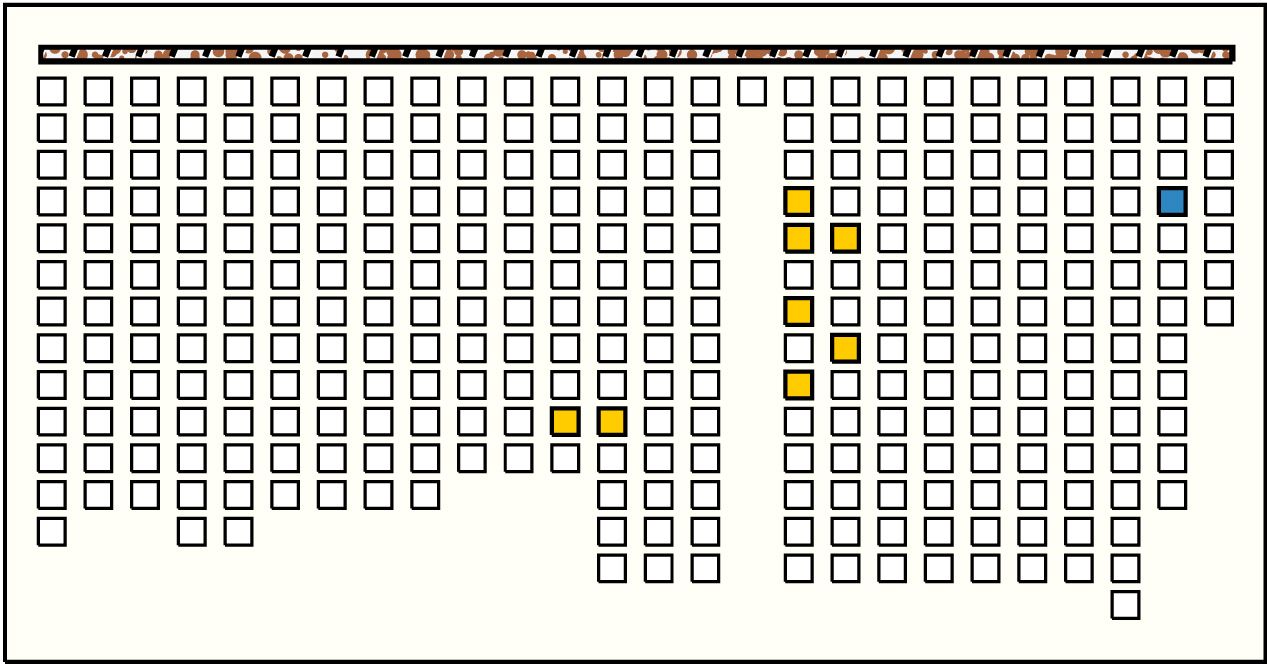p304_{25, 4} : 200_W:BY	200	8	p143: 33_W:BY + p154: 66_W:BY + p191: 10_W:BY + p192: 22_W:BY + p194: 32_W:BY + p196: 20_W:BY + p206: 6_W:BY + p209: 11_W:BY
8	p316_{26, 4} : 200_W-BY	200	7	p7: 33_W-BY + p19: 23_W-BY + p20: 33_W-BY + p32: 23_W-BY + p33: 33_W-BY + p44: 22_W-BY + p45: 33_W-BY

Khipu Notes:

Ashok Khosla's Notes:

Juliana Martins proposes that this is an astronomical khipu - see Martins

Ascher Databook Notes:

The finishing knot on P10 is knotted around P11. Thus, the end of P10 is tied to P11 at 5. 5 cm. from the bottom of P11.
Small spaces on the main cord appear between some adjacent pendants. The darkened color of the main cord at those points, leads us to assume that a pendant was present but is now missing. These hypothetical pendants are included in the listing but designated as missing.
By spacing, the khipu is separated into 25 groups but ends with a break in the main cord at the middle of the 25th group. A marker on the main cord separates the first 15 groups from the last 10 groups.

At first glance, the groups seem to vary in size and color pattern. However, when viewed as groups of 15 pendants with some positions non-existent in each group, the colors and values are repetitions. The 25 groups of 15 pendants have been arranged in a rectangular table (see Table 1). A blank means the position is non-existent, an M is a missing pendant, and a ? indicates that the pendant is broken so the value is unknown. An unequal sign ≠ has been used to mark a change in color. Where there is no color change, but just a color anomaly, the value has been grouped with parentheses i.e. (39). Observe from the table that although similarities remain, there are decided differences between part 1 (groups 1-15) and part 2 (groups 16-26). Also, within part 1, there are several changes after the 5th group and after the 12th group.

Table 1

Group Position	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
1	1080	12	22	100	40			23	33	65	33	12	11≠	42	456
2	1091	?	22	100	40			23	33	(76)	33	33		42	?
3	1078	12	21	?	?	M		23	33	66	32	33		42
4	1069	12	22	?	40	M		22	33	66	32	33		42	?≠
5	1077	(22)	22≠	?	50≠	M	≠	22	32	66	32	33		43	?
6	1078	12		100	50		222	22	33	()	32	33		42	?
7	1179	12≠		100	50		222	22	33	66	32	33		43	4??
8	1089	12		100	50		M	22	33	66	32	33		42	4??≠
9	1078	12		100	40		222	22	32	66	32	33		42	467
10	1087	(12)		100	40		222	22	32	()	22	33		42
11	1087	12		100	40		M	22	32	?	32	44		42
12	1065	12	≠	100≠	40	≠	?	22≠	32≠	M ≠	3?≠	(33)		(42)	-
13	912	11	0	100	(4?)	0	222	M	32	(66)	32	?		32
14	1030	21	0	100	M≠	0	222	32	32	66	32	?	≠	(42)
15	924	21	0	100	40	0	222	32	32	66	32	?	(M)	42
16	1356	12		200	10	(22)	32	32	M	(20)	?	44	(0)	34	8??
17	1164	(12)	?	200	6	22	21	11≠	21	21	?	31	(0)	22
18	1185	(25)	?	(200)	10	(12)	22	22	?	22	?	23	?	34
19	1015	13	43≠	1??	15	12	22	23	23	23	M	32≠	?	(34)
20	1575	14	?	200	(7)	32	64	64	54	54	M	32	?	22
21	1162	13	45	100	6	12	23	23	23	23	(?)	32	?	31
22	1385	12	?	100	10	22	43	34	3?	43	22	22	M	32
23	956	11	(?)	100	14	23	13	23	?	13	(?)	22	(?)	22	?
24	996	10	0	200	6	?	23	23	?	22	?	22
25	997	11	0	200	10	12