UR1151/KH0167 - Colored Pendant Sums


Drawings:
Overview Detail View
All Khipus' Ascher Sum FieldmarksRight-Handed XRay
All Colored Pendant Sum RelationshipsLeft-Handed XRay
This Khipu's Fieldmark CatalogRight-Handed Sum Detail
This Khipu's DrawingLeft-Handed Sum Detail

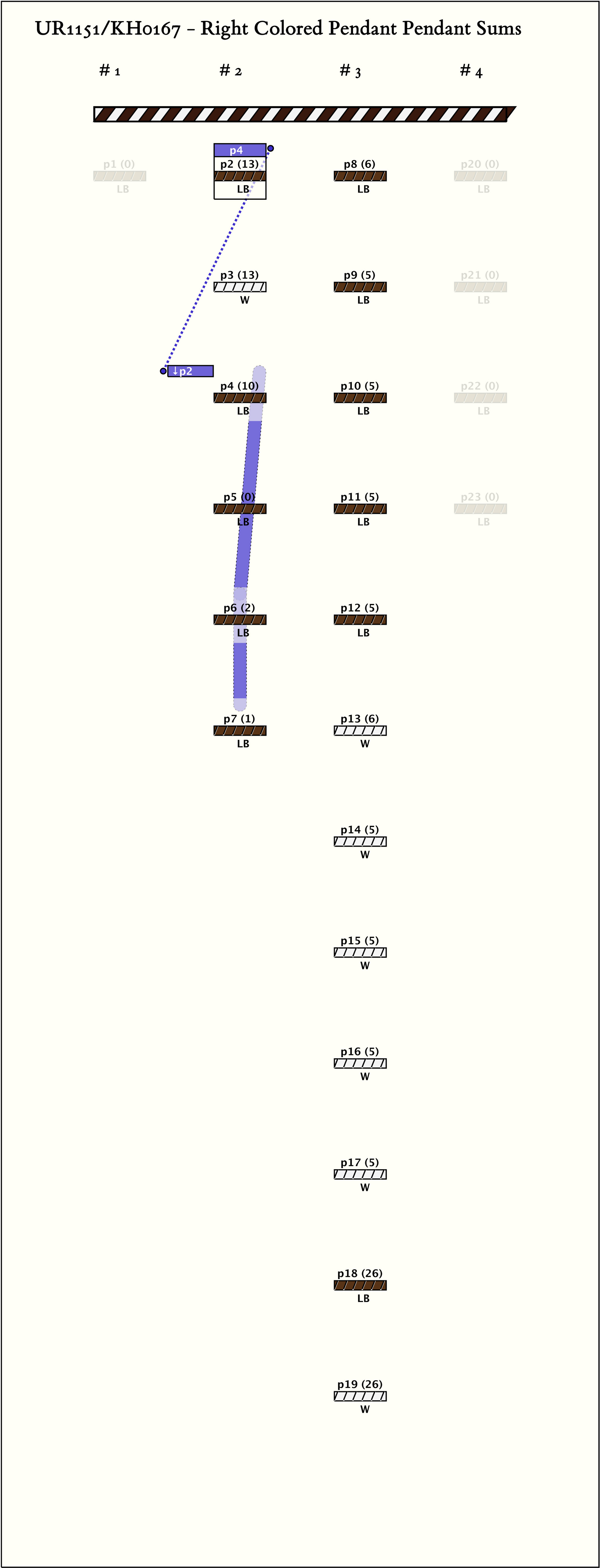
Right Handed Sums:     # Sums = 1,  Max # Summands = 3,   (Min, Mean, Max) Sum Values = (13, 13, 13)
Click on Image to View Larger

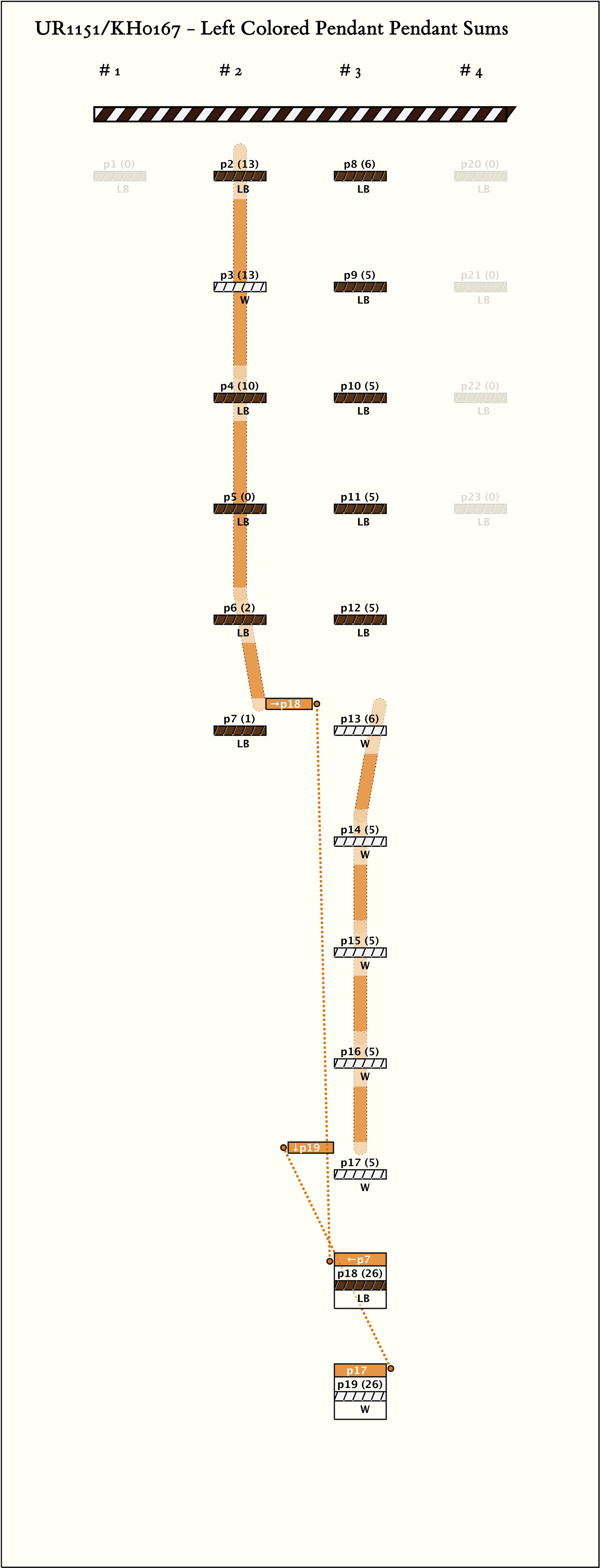
Left Handed Sums:     # Sums = 2,  Max # Summands = 5,   (Min, Mean, Max) Sum Values = (26, 26, 26)
Click on Image to View Larger

Right Handed Sum Detail: - Click on column name to sort
# Color Sum Schema Sum Cord Sum Cord Value # Summands Summands
1
p22, 1 : 13LB133p4: 10LB + p6: 2LB + p7: 1LB

Left Handed Sum Detail: - Click on column name to sort
# Color Sum Schema Sum Cord Sum Cord Value # Summands Summands
1
p183, 11 : 26LB264p2: 13LB + p4: 10LB + p6: 2LB + p7: 1LB
2
p193, 12 : 26W265p13: 6W + p14: 5W + p15: 5W + p16: 5W + p17: 5W

Khipu Notes:
Ascher Databook Notes:
  1. This is one of several khipus acquired by the Museum in 1907 with provenance Pachacamac. For a list of them, see UR1097.
  2. By spacing, the khipu is separated into 4 groups of 1, 6, 12, and 4 pendants respectively.
    1. The pendant in group 1 and the pendants in group 4 are LB and zero-valued (or blank). The subsidiaries in group 1 are W and non-zero.
    2. The 6 pendants of group 2 are one pair of pendants LB, Wand then 4 LB pendants each with a W subsidiary. Each of the values in the first pair is 13; the 4 LB pendant values sum to 13; and 4 W sub_sidiaries sum to 13.
    3. The 12 pendants of group 3 are 5 LB pendants with LB subsidiaries, then 5 W pendants with W subsidiaries, and then 1 pair of pendants LB, W each with a subsidiary of the same color. The first 5 LB pendant values sum to 26; then the 5 W pendant values sum to 26; and each of values in the last pair is 26. Excluding subsidiaries suspended from subsidiaries rather than from pendants, the subsidiaries also sum to 26.
    4. With the exception of the subsidiaries of subsidiaries of group 3, all the values in groups 2 and 3 are summarized in Table 1.

      Table 1

      Group Color LB Color W
      Group 2
      P21 = 13
      \[ \sum\limits_{i=3}^{6} P_{2i}\;=\;13 \]
      P22 = 13
      \[ \sum\limits_{i=3}^{6} P_{2i}\;subsidiaries\;=\;13 \]
      Group 3
      P3,11 = 26
      \[ \sum\limits_{i=1}^{5} P_{3i}\; = \;26 \]
      \[ \sum\limits_{i=1}^{5} P_{3i}\;\;subsidiaries\; = \;P_{3,11}\;subsidiary \]
      P3,12 = 26
      \[ \sum\limits_{i=6}^{10} P_{3i}\; = \;26 \]
      \[ \sum\limits_{i=1}^{5} P_{3i}\;\;subsidiaries\; = \;P_{3,12}\;subsidiary \]
      Group 3
      \[ \sum\limits_{i=1}^{10} P_{3i}\;\;subsidiaries\; = \;P_{3,11}\;subsidiary + P_{3,12}\;subsidiary = 26 \]