UR1140/KH0156 - Pendant Pendant Sums
Drawings:
Right Handed Sums: # Sums = 53, Max # Summands = 7, (Min, Mean, Max) Sum Values = (11, 40, 114)
Click on Image to View Larger
Left Handed Sums: # Sums = 49, Max # Summands = 6, (Min, Mean, Max) Sum Values = (11, 40, 114)
Click on Image to View Larger
Right Handed Sum Detail: - Click on column name to sort
| # | Color | Sum Schema | Sum Cord | Sum Cord Value | # Summands | Summands |
|---|---|---|---|---|---|---|
| 1 |  | p91, 9 : 96B | 96 | 4 | p22: 19B + p23: 29B + p24: 18B + p25: 30B | |
| 2 |  | p142, 5 : 22B | 22 | 3 | p60: 6B:BB + p61: 14B:BB + p62: 2B | |
| 3 |  | p162, 7 : 17B | 17 | 2 | p59: 11B + p60: 6B:BB | |
| 4 |  | p182, 9 : 91B | 91 | 5 | p28: 20B + p29: 25B + p30: 20B + p31: 15B + p32: 11B | |
| 5 |  | p203, 2 : 13B | 13 | 2 | p34: 11B + p35: 2B | |
| 6 |  | p223, 4 : 19B | 19 | 2 | p55: 9B + p56: 10B | |
| 7 |  | p233, 5 : 29B | 29 | 2 | p58: 18B + p59: 11B | |
| 8 |  | p273, 9 : 95B | 95 | 2 | p62: 2B + p63: 93B | |
| 9 |  | p304, 3 : 20B | 20 | 2 | p60: 6B:BB + p61: 14B:BB | |
| 10 |  | p364, 9 : 90B | 90 | 4 | p38: 32B + p39: 23B + p40: 23B + p41: 12B | |
| 11 |  | p375, 1 : 34B | 34 | 2 | p57: 16B + p58: 18B | |
| 12 |  | p455, 9 : 98B | 98 | 4 | p47: 36B + p48: 26B + p49: 26B + p50: 10B | |
| 13 |  | p496, 4 : 26B | 26 | 2 | p56: 10B + p57: 16B | |
| 14 |  | p516, 6 : 15B | 15 | 2 | p68: 10B + p69: 5B:BB | |
| 15 |  | p546, 9 : 79B | 79 | 3 | p76: 45B + p77: 16B + p78: 18B:BB | |
| 16 |  | p678, 4 : 36B | 36 | 2 | p114: 20B:G + p115: 16B | |
| 17 |  | p728, 9 : 93B | 93 | 4 | p117: 12B + p118: 32B + p119: 15B + p120: 34B | |
| 18 |  | p769, 4 : 45B | 45 | 5 | p124: 6B + p125: 18B + p126: 10B + p127: 6B + p128: 5B | |
| 19 |  | p819, 9 : 98B | 98 | 2 | p101: 35B + p102: 63B | |
| 20 |  | p8410, 3 : 28B | 28 | 2 | p103: 6B + p104: 22B:G | |
| 21 |  | p8810, 7 : 18B:BB | 18 | 2 | p122: 6B:G + p123: 12B:G | |
| 22 |  | p9010, 9 : 96B | 96 | 5 | p115: 16B + p116: 21B + p117: 12B + p118: 32B + p119: 15B | |
| 23 |  | p9312, 1 : 114B | 114 | 5 | p116: 21B + p117: 12B + p118: 32B + p119: 15B + p120: 34B | |
| 24 |  | p9512, 3 : 23B:G | 23 | 2 | p153: 11B + p154: 12B | |
| 25 |  | p9612, 4 : 24B:G | 24 | 3 | p122: 6B:G + p123: 12B:G + p124: 6B | |
| 26 | 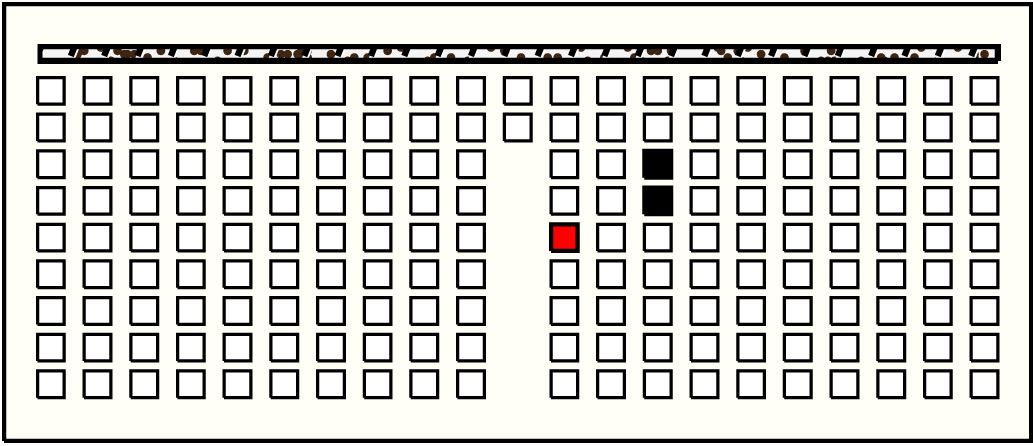 | p9712, 5 : 31B | 31 | 2 | p113: 11B:G + p114: 20B:G | |
| 27 | 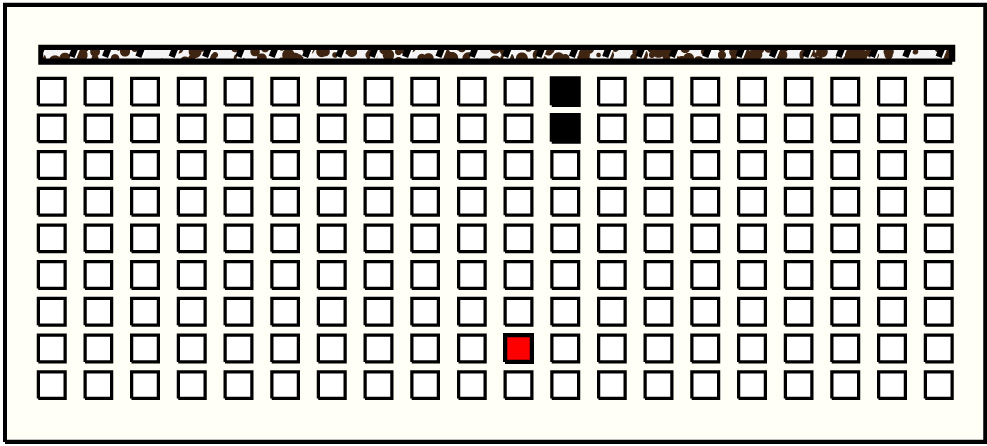 | p9812, 6 : 30B | 30 | 2 | p131: 11B:BB + p132: 19B:BB | |
| 28 |  | p10012, 8 : 69B | 69 | 2 | p102: 63B + p103: 6B | |
| 29 | 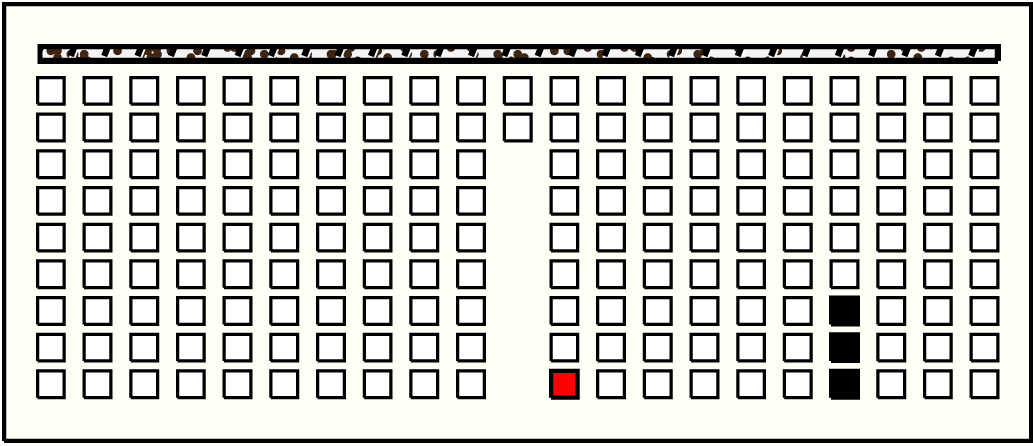 | p10112, 9 : 35B | 35 | 3 | p153: 11B + p154: 12B + p155: 12B | |
| 30 |  | p10213, 1 : 63B | 63 | 7 | p122: 6B:G + p123: 12B:G + p124: 6B + p125: 18B + p126: 10B + p127: 6B + p128: 5B | |
| 31 | 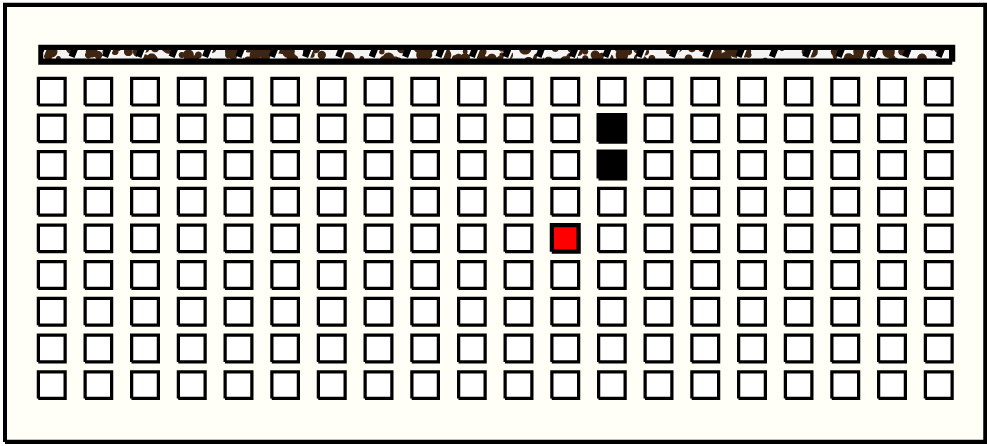 | p10413, 3 : 22B:G | 22 | 3 | p121: 4B + p122: 6B:G + p123: 12B:G | |
| 32 | 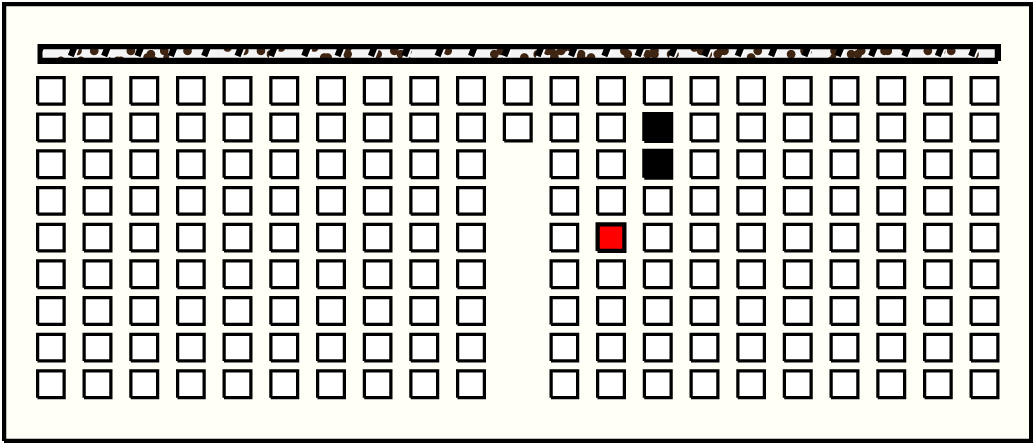 | p10613, 5 : 17B | 17 | 2 | p112: 6B + p113: 11B:G | |
| 33 | 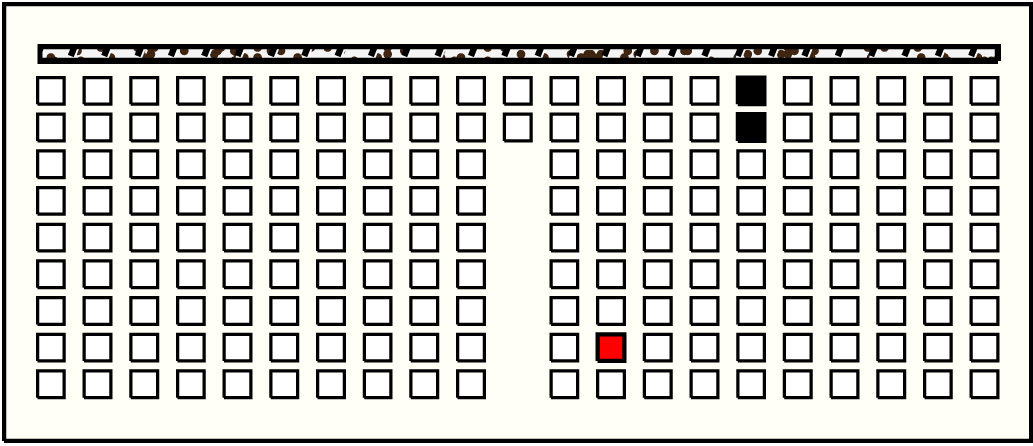 | p10913, 8 : 61B | 61 | 2 | p129: 53B + p130: 8B | |
| 34 | 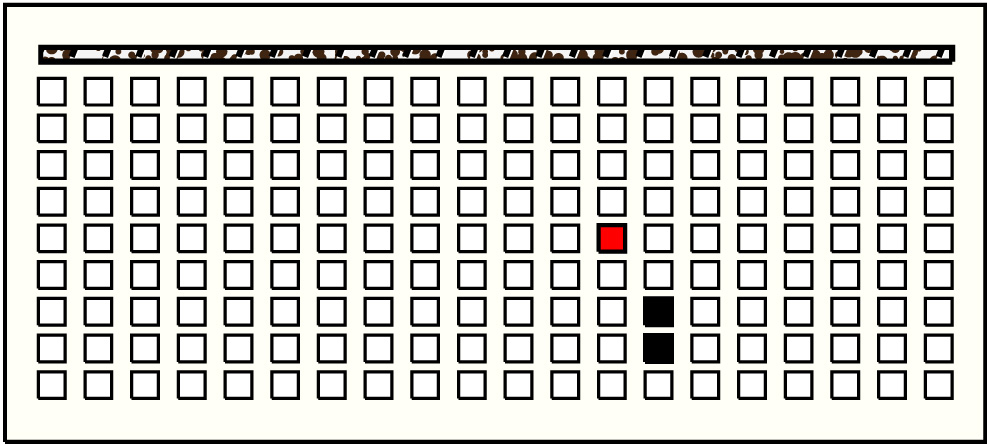 | p11314, 3 : 11B:G | 11 | 2 | p127: 6B + p128: 5B | |
| 35 | 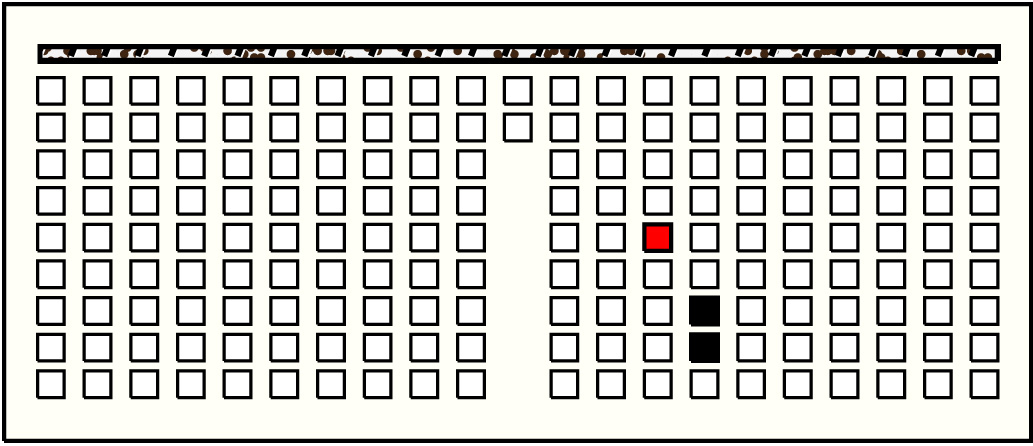 | p11514, 5 : 16B | 16 | 2 | p126: 10B + p127: 6B | |
| 36 |  | p11614, 6 : 21B | 21 | 3 | p126: 10B + p127: 6B + p128: 5B | |
| 37 | 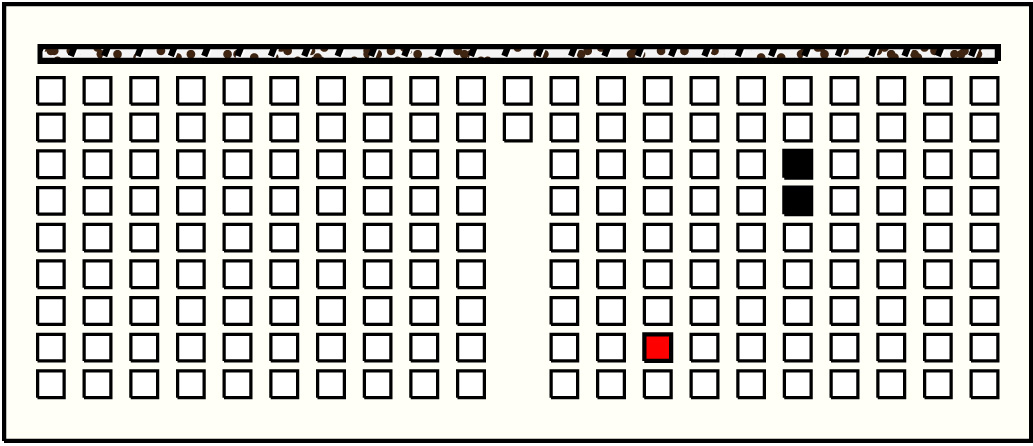 | p11814, 8 : 32B | 32 | 2 | p140: 10B:BB + p141: 22B:BB | |
| 38 | 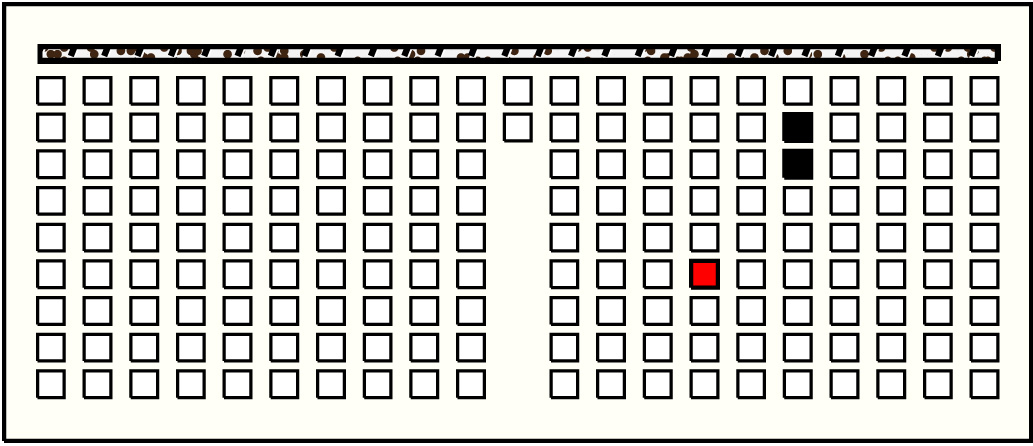 | p12515, 6 : 18B | 18 | 2 | p139: 8B + p140: 10B:BB | |
| 39 | 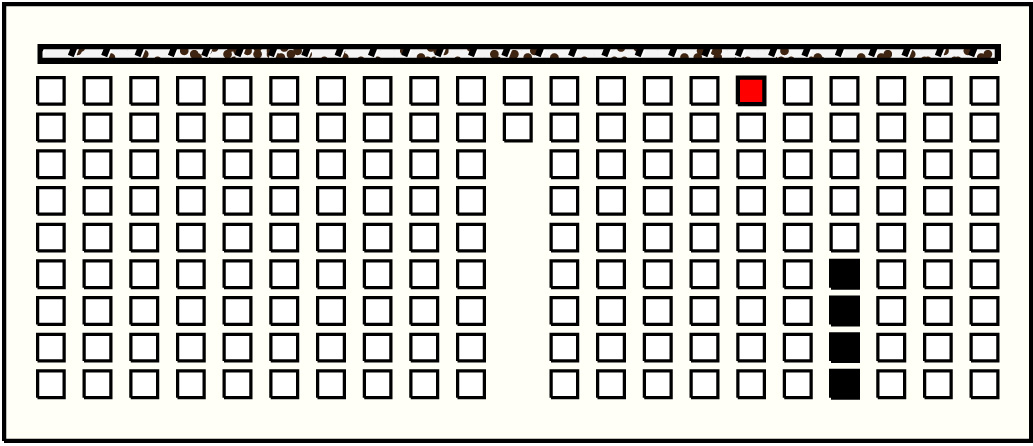 | p12916, 1 : 53B | 53 | 4 | p152: 18B + p153: 11B + p154: 12B + p155: 12B | |
| 40 |  | p13216, 4 : 19B:BB | 19 | 2 | p181: 11B + p182: 8B | |
| 41 | 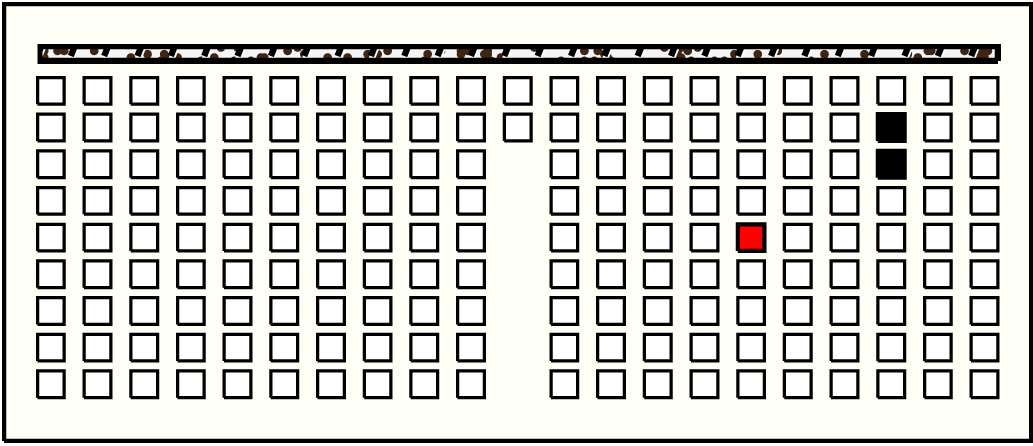 | p13316, 5 : 25B | 25 | 2 | p157: 8B + p158: 17B:BB | |
| 42 |  | p13416, 6 : 24B | 24 | 2 | p154: 12B + p155: 12B | |
| 43 | 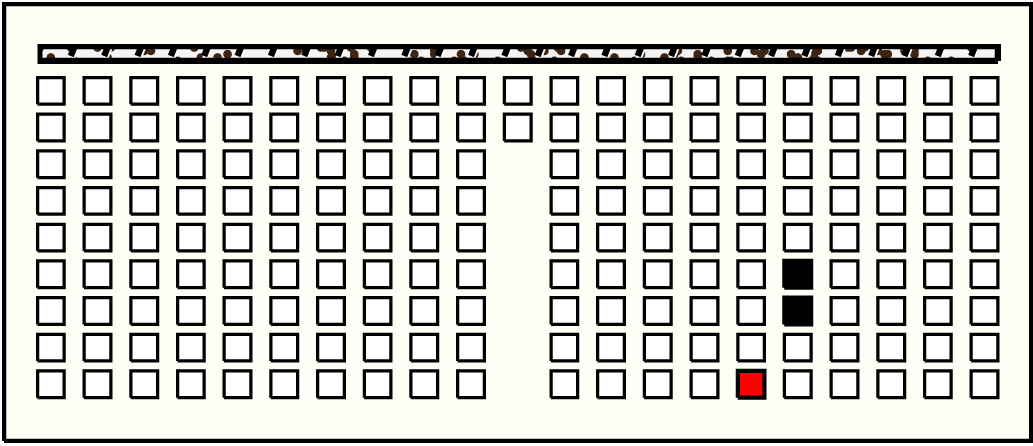 | p13716, 9 : 21B | 21 | 2 | p143: 18B + p144: 3B | |
| 44 |  | p14117, 4 : 22B:BB | 22 | 2 | p149: 11B:BB + p150: 11B:BB | |
| 45 |  | p14317, 6 : 18B | 18 | 2 | p148: 7B + p149: 11B:BB | |
| 46 |  | p14517, 8 : 27B | 27 | 2 | p177: 14B:BB + p178: 13B | |
| 47 | 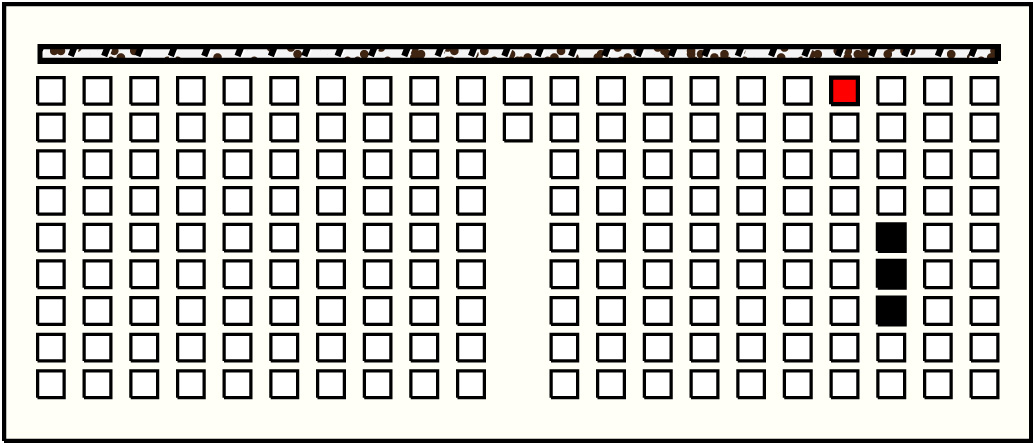 | p14718, 1 : 56B | 56 | 3 | p160: 23B + p161: 20B + p162: 13B | |
| 48 | 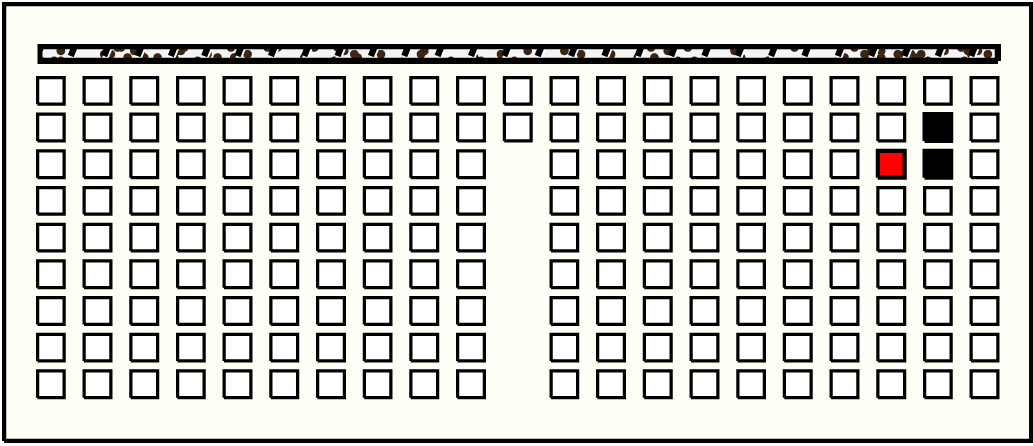 | p15819, 3 : 17B:BB | 17 | 2 | p166: 4B + p167: 13B:BB | |
| 49 |  | p15919, 4 : 18B:BB | 18 | 2 | p167: 13B:BB + p168: 5B:BB | |
| 50 |  | p16119, 6 : 20B | 20 | 2 | p171: 4B + p172: 16B | |
| 51 |  | p16319, 8 : 37B | 37 | 3 | p168: 5B:BB + p169: 11B + p170: 21B | |
| 52 | 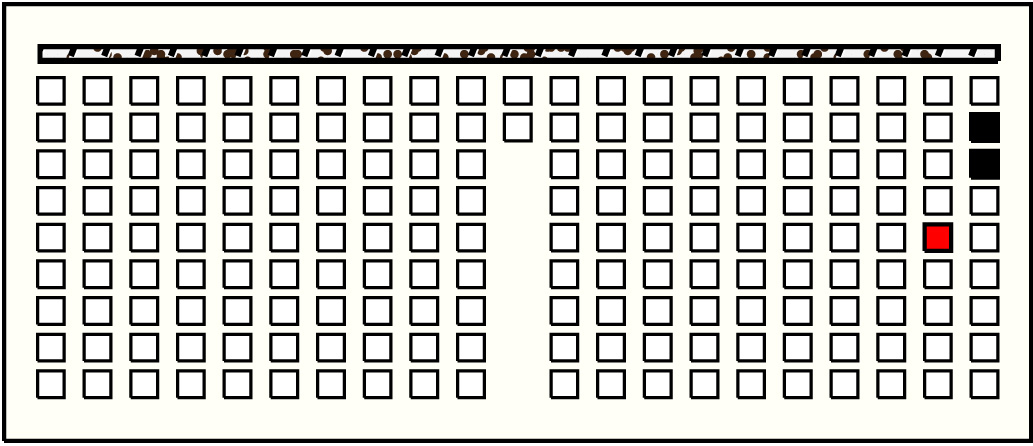 | p16920, 5 : 11B | 11 | 2 | p175: 4B + p176: 7B:BB | |
| 53 |  | p17020, 6 : 21B | 21 | 2 | p176: 7B:BB + p177: 14B:BB |
Left Handed Sum Detail: - Click on column name to sort
| # | Color | Sum Schema | Sum Cord | Sum Cord Value | # Summands | Summands |
|---|---|---|---|---|---|---|
| 1 |  | p193, 1 : 16B | 16 | 2 | p1: 3B + p2: 13B | |
| 2 |  | p253, 7 : 30B | 30 | 2 | p12: 20B + p13: 10B | |
| 3 |  | p273, 9 : 95B | 95 | 2 | p17: 4B + p18: 91B | |
| 4 |  | p375, 1 : 34B | 34 | 2 | p4: 22B + p5: 12B | |
| 5 |  | p385, 2 : 32B | 32 | 2 | p13: 10B + p14: 22B | |
| 6 |  | p455, 9 : 98B | 98 | 2 | p26: 3B + p27: 95B | |
| 7 |  | p476, 2 : 36B | 36 | 3 | p5: 12B + p6: 14B + p7: 10B | |
| 8 |  | p486, 3 : 26B | 26 | 2 | p33: 15B + p34: 11B | |
| 9 |  | p546, 9 : 79B | 79 | 6 | p2: 13B + p3: 8B + p4: 22B + p5: 12B + p6: 14B + p7: 10B | |
| 10 |  | p617, 7 : 14B:BB | 14 | 2 | p7: 10B + p8: 4B | |
| 11 |  | p648, 1 : 22B | 22 | 3 | p60: 6B:BB + p61: 14B:BB + p62: 2B | |
| 12 |  | p678, 4 : 36B | 36 | 2 | p49: 26B + p50: 10B | |
| 13 |  | p708, 7 : 17B:BB | 17 | 2 | p59: 11B + p60: 6B:BB | |
| 14 |  | p749, 2 : 41B | 41 | 3 | p31: 15B + p32: 11B + p33: 15B | |
| 15 |  | p759, 3 : 15B | 15 | 2 | p68: 10B + p69: 5B:BB | |
| 16 |  | p769, 4 : 45B | 45 | 3 | p57: 16B + p58: 18B + p59: 11B | |
| 17 |  | p779, 5 : 16B | 16 | 2 | p61: 14B:BB + p62: 2B | |
| 18 |  | p819, 9 : 98B | 98 | 3 | p54: 79B + p55: 9B + p56: 10B | |
| 19 |  | p8210, 1 : 31B | 31 | 3 | p59: 11B + p60: 6B:BB + p61: 14B:BB | |
| 20 |  | p8410, 3 : 28B | 28 | 3 | p33: 15B + p34: 11B + p35: 2B | |
| 21 |  | p8510, 4 : 43B | 43 | 2 | p42: 25B + p43: 18B | |
| 22 |  | p8610, 5 : 35B | 35 | 3 | p58: 18B + p59: 11B + p60: 6B:BB | |
| 23 |  | p8910, 8 : 22B | 22 | 2 | p69: 5B:BB + p70: 17B:BB | |
| 24 |  | p9010, 9 : 96B | 96 | 4 | p22: 19B + p23: 29B + p24: 18B + p25: 30B | |
| 25 | 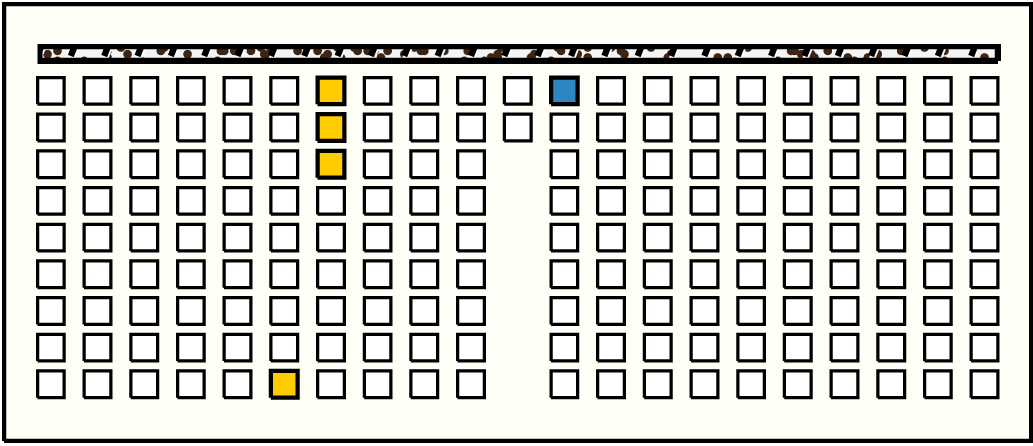 | p9312, 1 : 114B | 114 | 4 | p54: 79B + p55: 9B + p56: 10B + p57: 16B | |
| 26 | 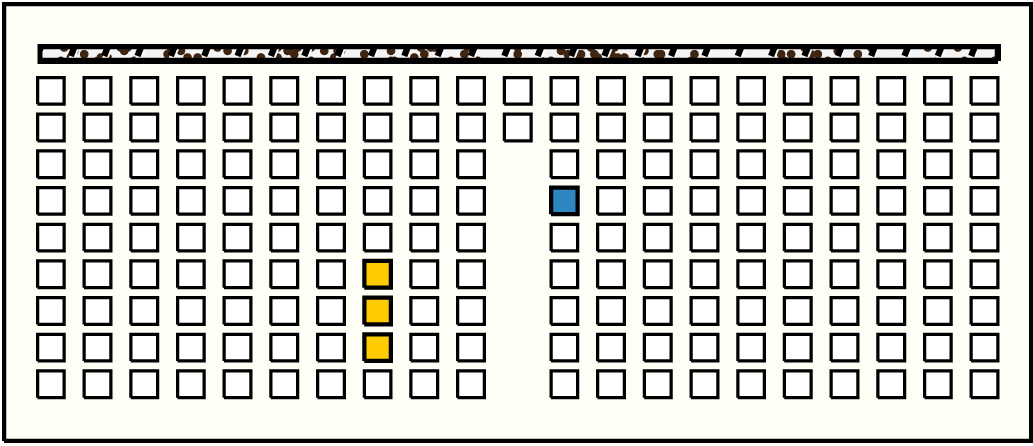 | p9612, 4 : 24B:G | 24 | 3 | p69: 5B:BB + p70: 17B:BB + p71: 2B | |
| 27 | 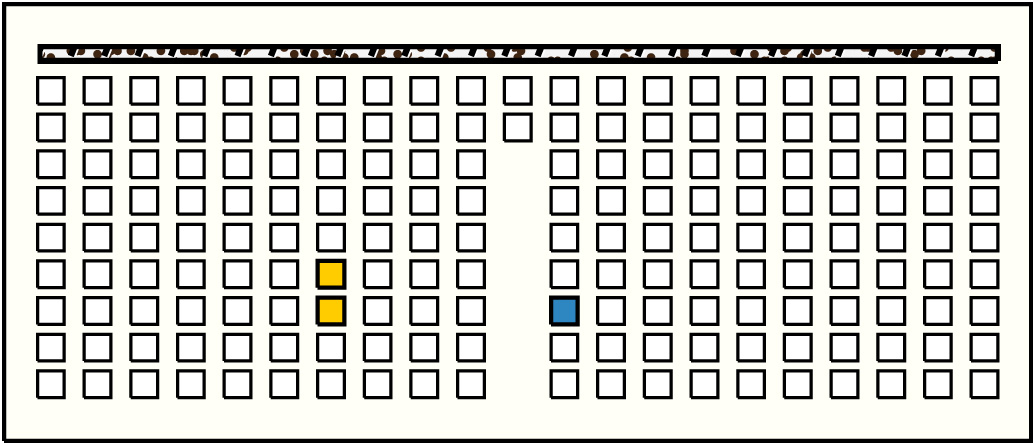 | p9912, 7 : 20B | 20 | 2 | p60: 6B:BB + p61: 14B:BB | |
| 28 |  | p10012, 8 : 69B | 69 | 5 | p2: 13B + p3: 8B + p4: 22B + p5: 12B + p6: 14B | |
| 29 | 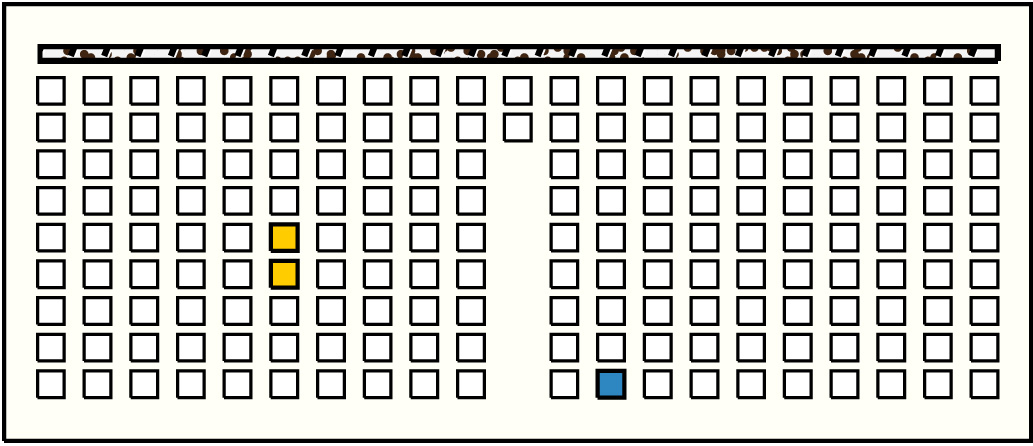 | p11013, 9 : 25B | 25 | 2 | p50: 10B + p51: 15B | |
| 30 | 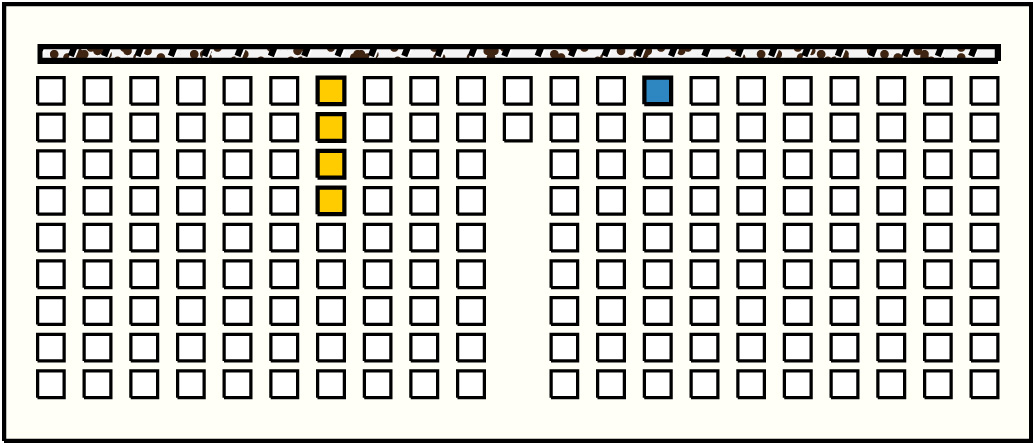 | p11114, 1 : 53B | 53 | 4 | p55: 9B + p56: 10B + p57: 16B + p58: 18B | |
| 31 |  | p11614, 6 : 21B | 21 | 2 | p87: 3B:BB + p88: 18B:BB | |
| 32 |  | p11814, 8 : 32B | 32 | 3 | p68: 10B + p69: 5B:BB + p70: 17B:BB | |
| 33 | 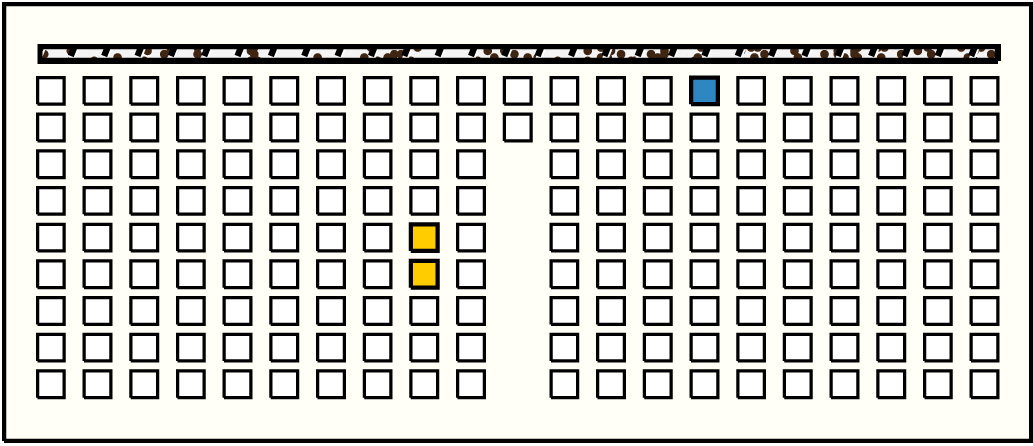 | p12015, 1 : 34B | 34 | 2 | p77: 16B + p78: 18B:BB | |
| 34 |  | p12916, 1 : 53B | 53 | 3 | p119: 15B + p120: 34B + p121: 4B | |
| 35 | 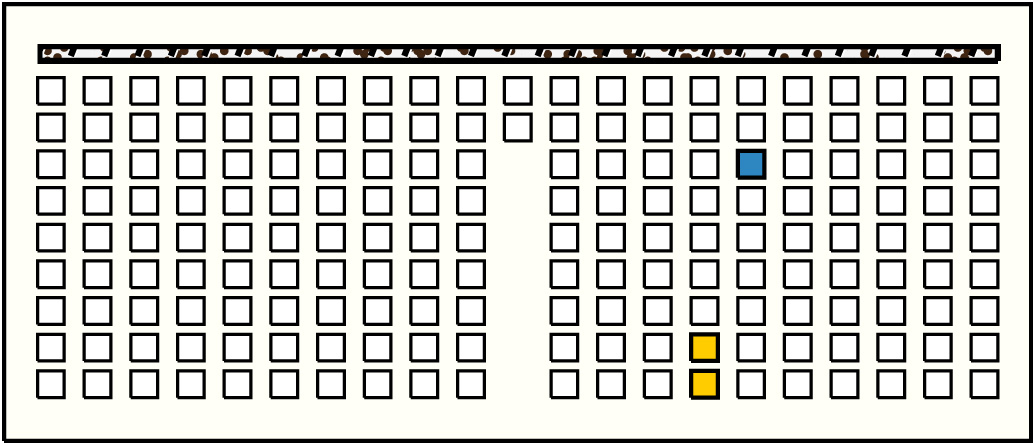 | p13116, 3 : 11B:BB | 11 | 2 | p127: 6B + p128: 5B | |
| 36 | 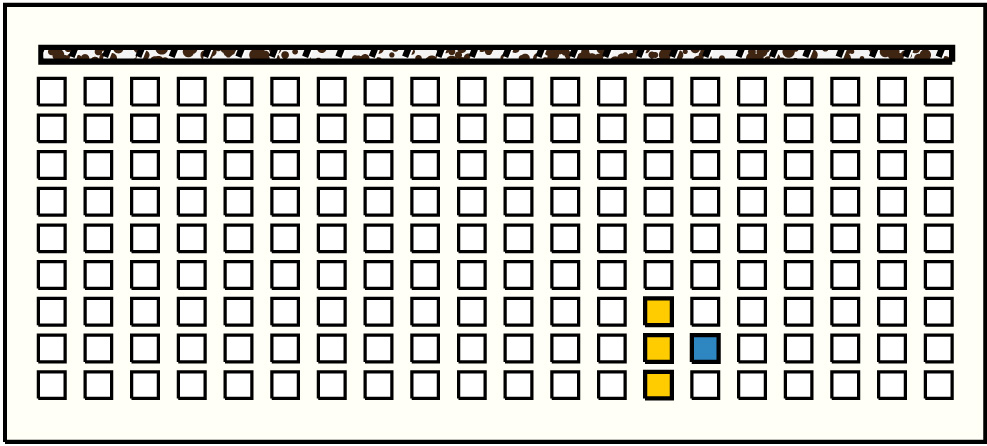 | p13416, 6 : 24B | 24 | 2 | p124: 6B + p125: 18B | |
| 37 |  | p13616, 8 : 21B | 21 | 3 | p126: 10B + p127: 6B + p128: 5B | |
| 38 | 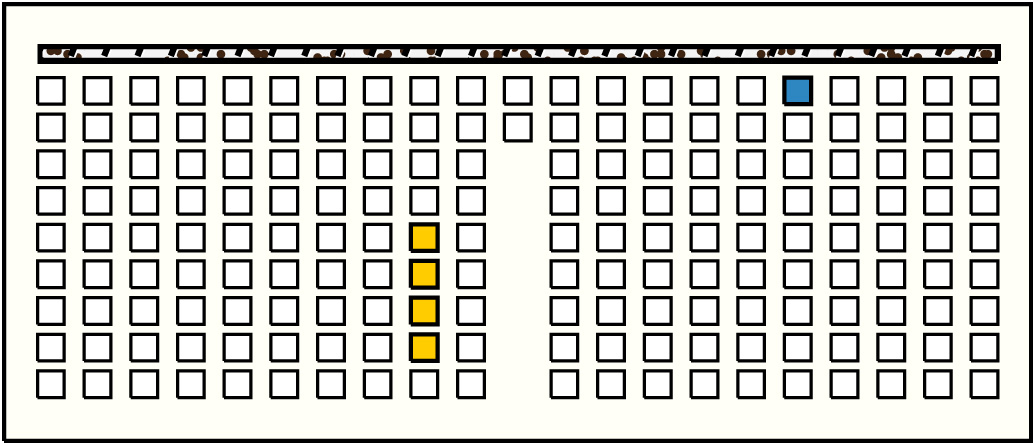 | p13817, 1 : 75B | 75 | 4 | p77: 16B + p78: 18B:BB + p79: 30B:BB + p80: 11B | |
| 39 | 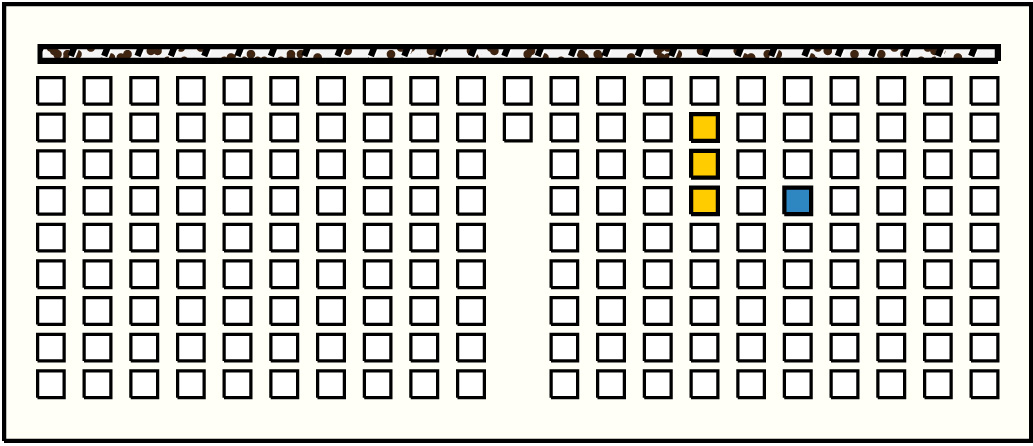 | p14117, 4 : 22B:BB | 22 | 3 | p121: 4B + p122: 6B:G + p123: 12B:G | |
| 40 |  | p14517, 8 : 27B | 27 | 2 | p107: 16B + p108: 11B | |
| 41 | 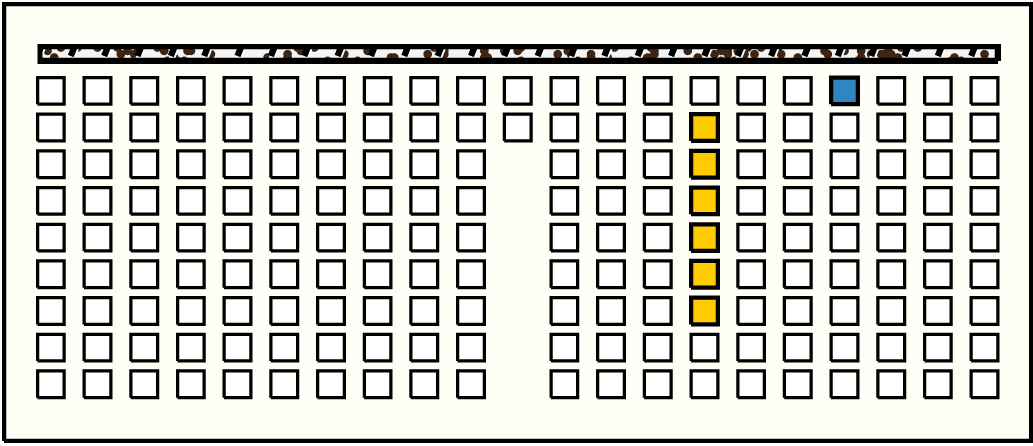 | p14718, 1 : 56B | 56 | 6 | p121: 4B + p122: 6B:G + p123: 12B:G + p124: 6B + p125: 18B + p126: 10B | |
| 42 |  | p15619, 1 : 70B | 70 | 3 | p111: 53B + p112: 6B + p113: 11B:G | |
| 43 |  | p15819, 3 : 17B:BB | 17 | 2 | p112: 6B + p113: 11B:G | |
| 44 |  | p16019, 5 : 23B | 23 | 2 | p153: 11B + p154: 12B | |
| 45 | 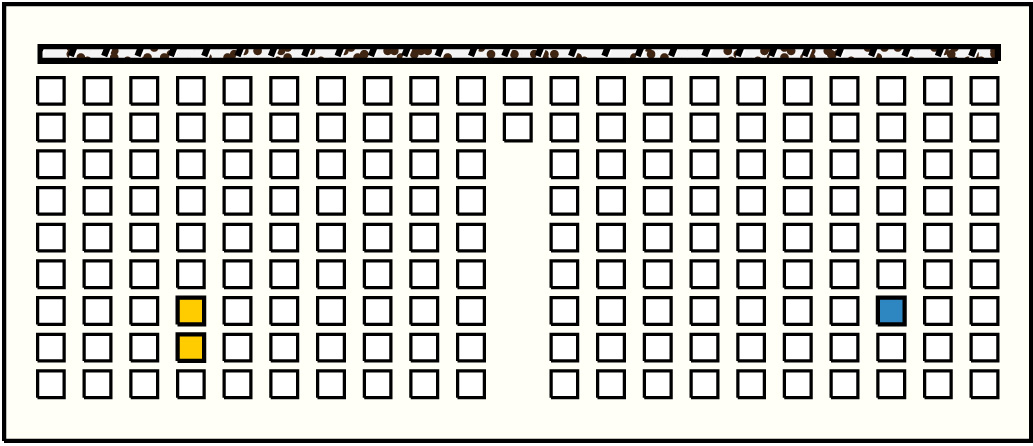 | p16219, 7 : 13B | 13 | 2 | p34: 11B + p35: 2B | |
| 46 |  | p16319, 8 : 37B | 37 | 2 | p115: 16B + p116: 21B | |
| 47 | 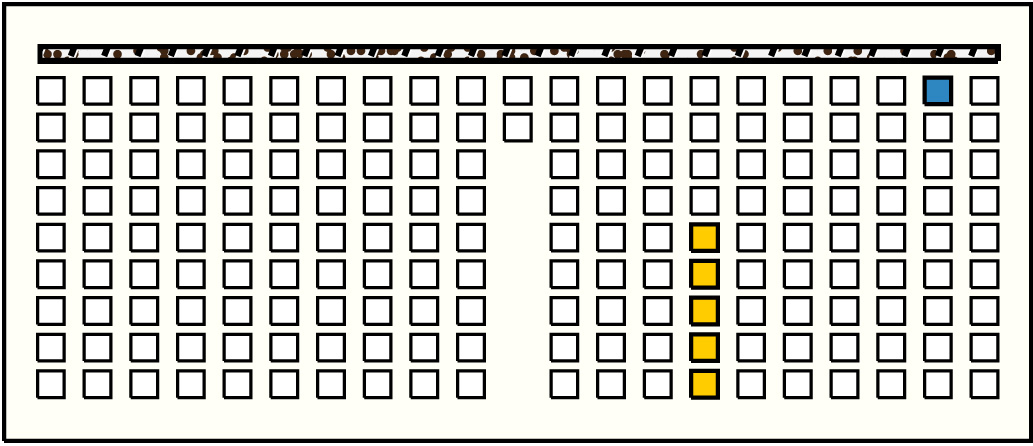 | p16520, 1 : 45B | 45 | 5 | p124: 6B + p125: 18B + p126: 10B + p127: 6B + p128: 5B | |
| 48 | 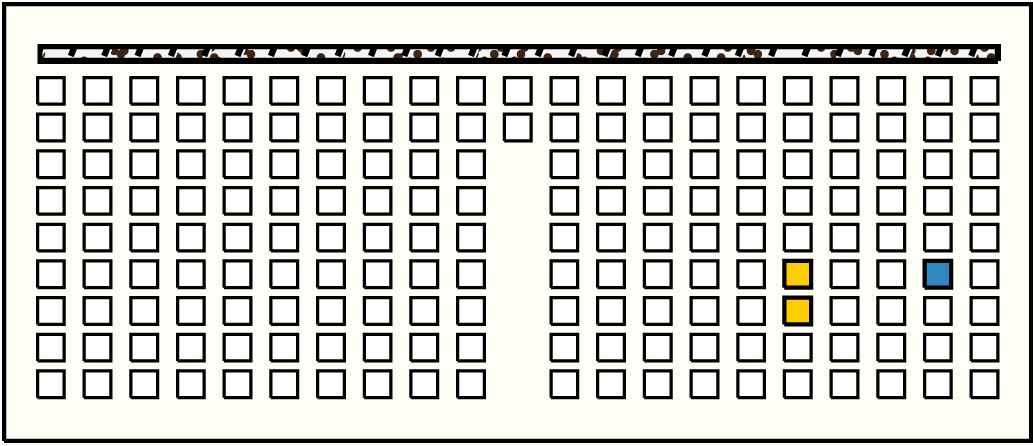 | p17020, 6 : 21B | 21 | 2 | p143: 18B + p144: 3B | |
| 49 | 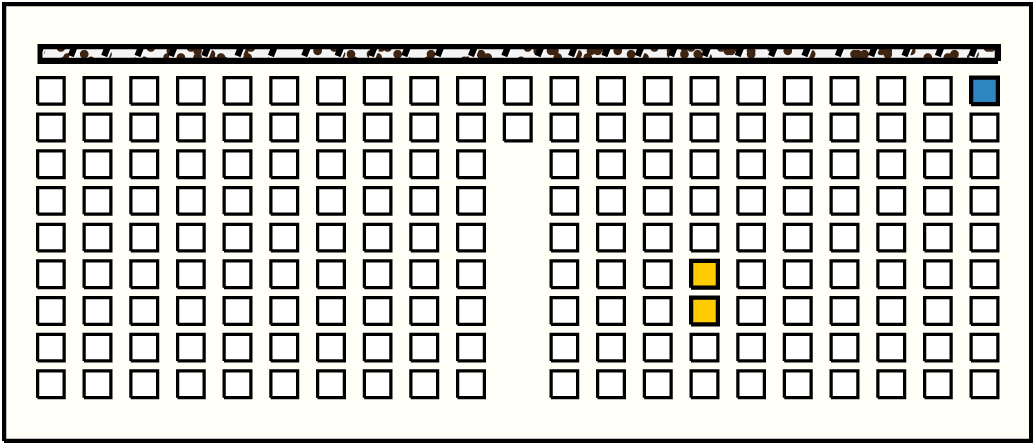 | p17421, 1 : 28B | 28 | 2 | p125: 18B + p126: 10B |
Khipu Notes:
This khipu has been entered with a strange nonconsecutive numbering scheme, indicating either the clusters are off, or the pendants are misnumbered. Investigation into the databook is warranted.
Ascher Databook Notes:
- The khipu is attached to a carved wooden bar.
- UR1136 and UR1140 were acquired by the Museum in 1904. The provenance is given as Nasca. For a comparison of them, see UR1136.
- UR1140 is discussed by Nordenskiold (see Introduction) .A photograph of it appears in Schmidt, Max, 1929, Kunst und Kultur von Peru, Impropyläen-Verlagzu, Berlin.
- The way in which the bar is threaded separates the khipu into 2 parts each containing 10 groups of 9 pendants each
Note: The pendant order on the listing proceeds from one end of the bar to the other, goes around the end, and continues on the other side. However, similar color and number patterns are found in both parts if the pendants are read instead from one end of the bar to the other, and then beginning at the original end on the other side of the bar. We will, therefore, refer to the pendants and groups on side 2 as if following the second scenario. Part 1 is pendants 1--->90 and references to the jth pendant in the ith group correspond to pendant 9 (i-1) +j. Part 2 is pendants 180--->91 and references to the jth pendant in the ith group correspond to pendant 190-9i-j.
By color, each part is separated into 2 subparts of 6 groups and 4 groups respectively. Each group has the same color pattern: 5 B, 2 mixed, 2 B. In the first 6 groups in part 1, the 2 mixed cords are B:BB/B, and in the last 4 groups they are B:BB. In the first 6 groups in part 2, the 2 mixed cords are B:BB, and in the last 4 groups they are B:G.
- Subsidiaries are only on the last pendant in each group in part 1. All are BB.
- In all groups in both parts:
- The last pendant in each group has the maximum value.
- With the exception of group 10 in part 1, the value on pendant 7 is always great than the value on pendant 8.
- Within part 1:
- For the 6 groups of the first subpart, the sum of the values in the 5th position equals the sum of the values in the 4th position. That is:
\[ \sum\limits_{i=1}^{6} P_{i5} = \sum\limits_{i=1}^{6} P_{i6} \] - For the 4 groups of the second subpart, the sum of the values in the first position equals the sum of the values in the second position.
\[ \sum\limits_{i=7}^{10} P_{i1} = \sum\limits_{i=7}^{10} P_{i2} \] - Excluding the last pendant in each group, the sum of the values in the first group equals the sum of the values in the corresponding group in the second subpart (group 7).
\[ \sum\limits_{j=1}^{8} P_{1j} = \sum\limits_{j=1}^{8} P_{7j} \]
- For the 6 groups of the first subpart, the sum of the values in the 5th position equals the sum of the values in the 4th position. That is:

