UR1152/KH0168 - Pendant Pendant Sums

Drawings:

Overview	Detail View
All Khipus' Ascher Sum Fieldmarks	Right-Handed XRay
All Pendant Pendant Sum Relationships	Left-Handed XRay
This Khipu's Fieldmark Catalog	Right-Handed Sum Detail
This Khipu's Drawing	Left-Handed Sum Detail

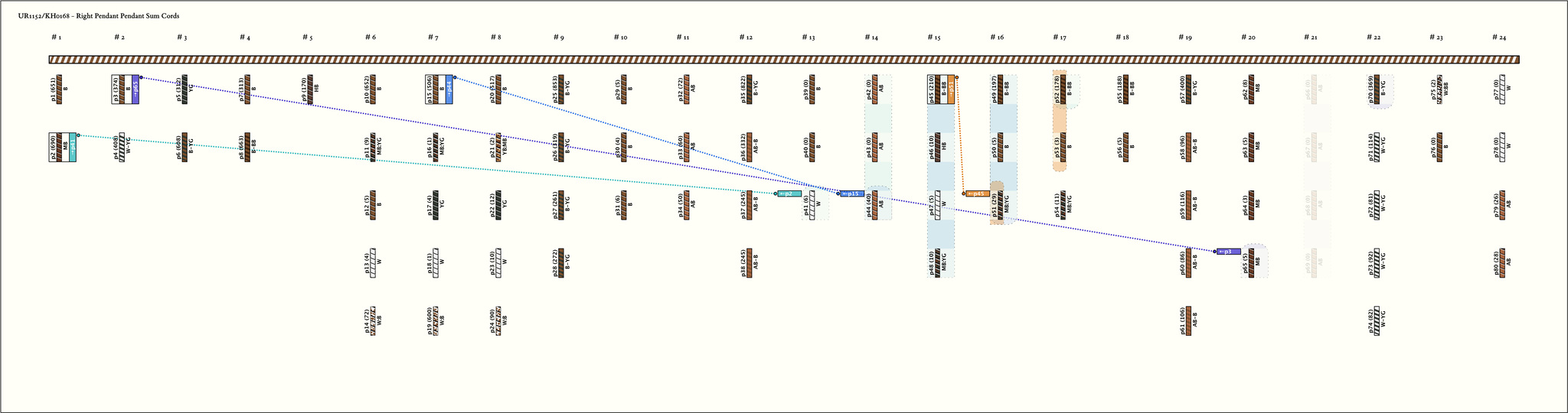
Right Handed Sums: # Sums = 4, Max # Summands = 12, (Min, Mean, Max) Sum Values = (210, 445, 690)
Click on Image to View Larger

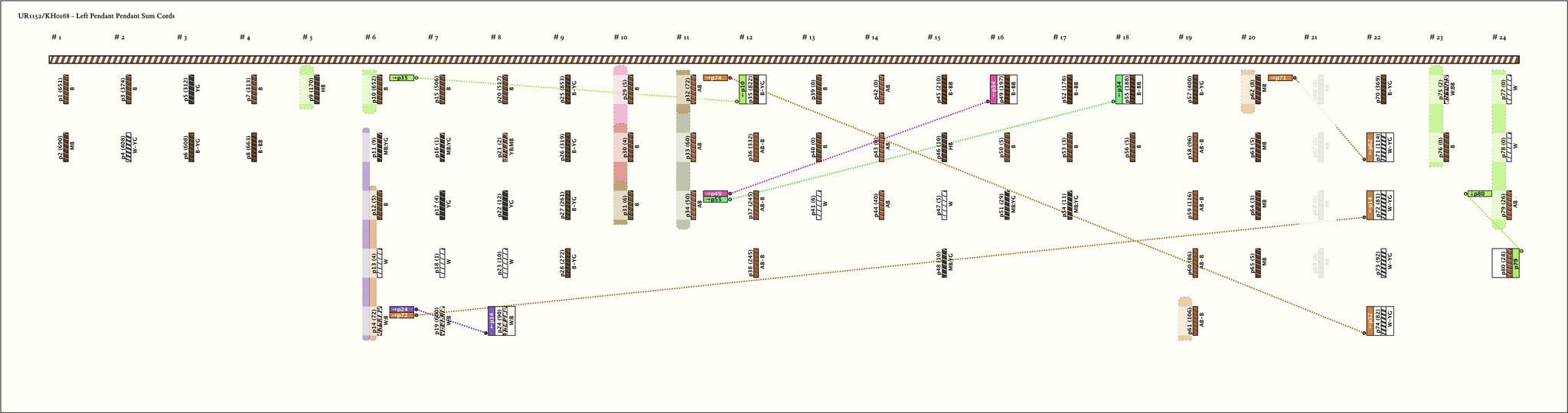
Left Handed Sums: # Sums = 8, Max # Summands = 6, (Min, Mean, Max) Sum Values = (28, 200, 822)
Click on Image to View Larger

Right Handed Sum Detail: - Click on column name to sort

#	Sum Cord	Sum Cord Value	# Summands	Summands
1	p2_{1, 2} : 690_MB	690	12	p41: 6_W + p42: 0_AB + p43: 0_AB + p44: 40_AB + p45: 210_B-BB + p46: 10_HB + p47: 5_W + p48: 10_MB:YG + p49: 197_B-BB + p50: 5_B + p51: 29_MB:YG + p52: 178_B-BB
2	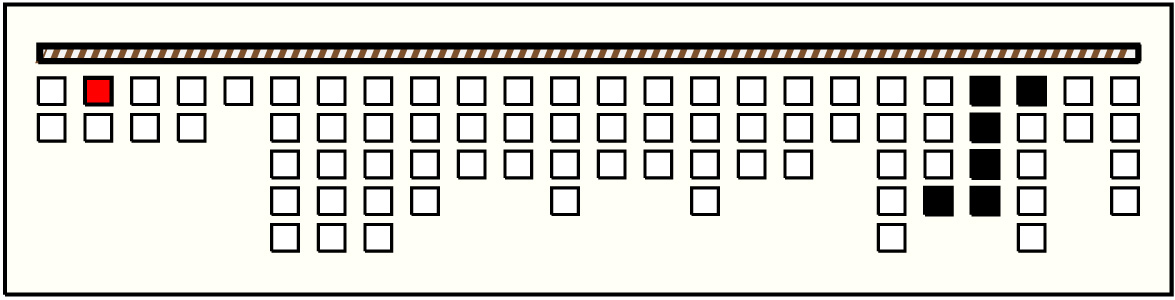p3_{2, 1} : 374_B	374	6	p65: 5_MB + p66: 0_AB + p67: 0_AB + p68: 0_AB + p69: 0_AB + p70: 369_B-YG
3	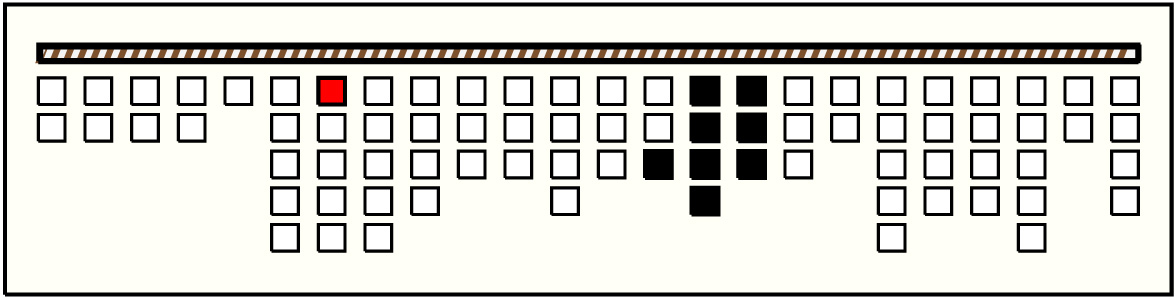p15_{7, 1} : 506_B	506	8	p44: 40_AB + p45: 210_B-BB + p46: 10_HB + p47: 5_W + p48: 10_MB:YG + p49: 197_B-BB + p50: 5_B + p51: 29_MB:YG
4	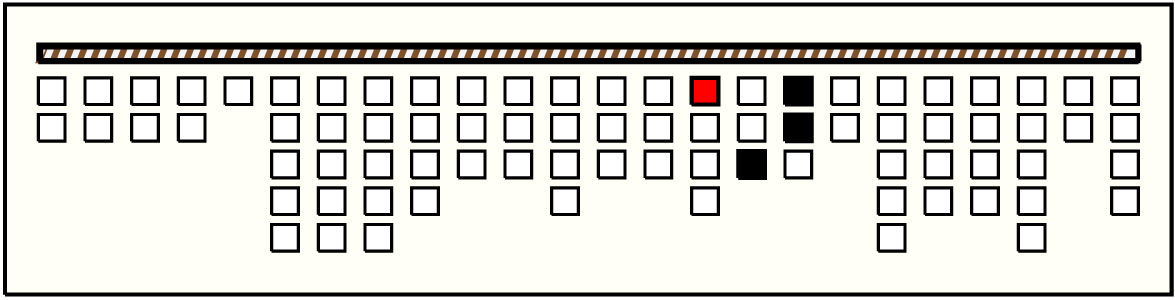p45_{15, 1} : 210_B-BB	210	3	p51: 29_MB:YG + p52: 178_B-BB + p53: 3_B

Left Handed Sum Detail: - Click on column name to sort

#	Sum Cord	Sum Cord Value	# Summands	Summands
1	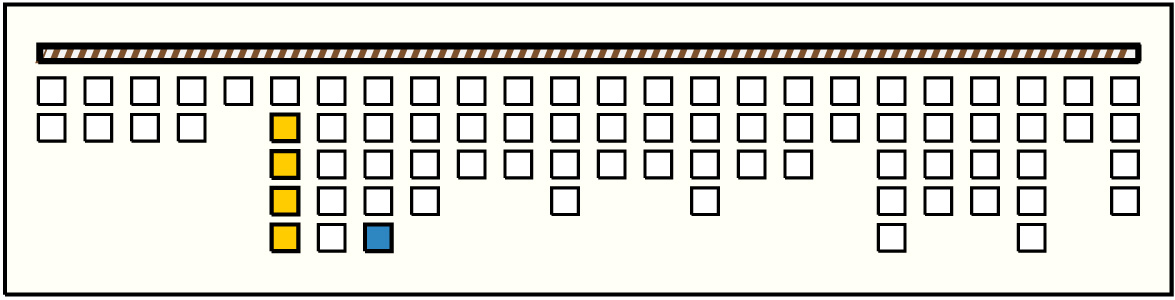p24_{8, 5} : 90_W:B	90	4	p11: 9_MB:YG + p12: 5_B + p13: 4_W + p14: 72_W:B
2	p35_{12, 1} : 822_B-YG	822	2	p9: 170_HB + p10: 652_B
3	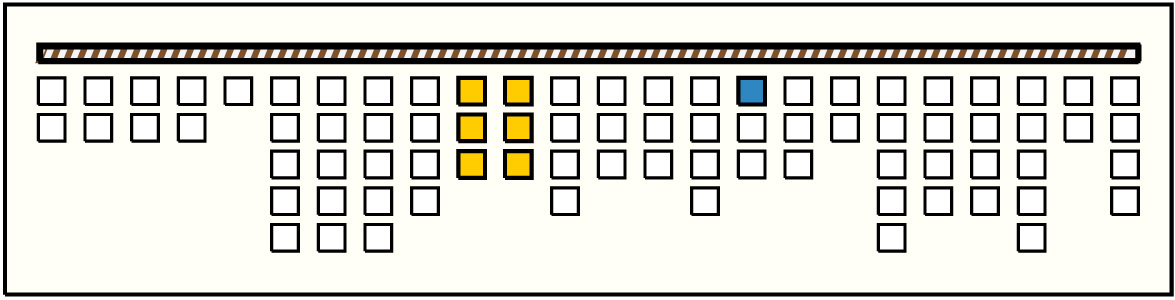p49_{16, 1} : 197_B-BB	197	6	p29: 5_B + p30: 4_B + p31: 6_B + p32: 72_AB + p33: 60_AB + p34: 50_AB
4	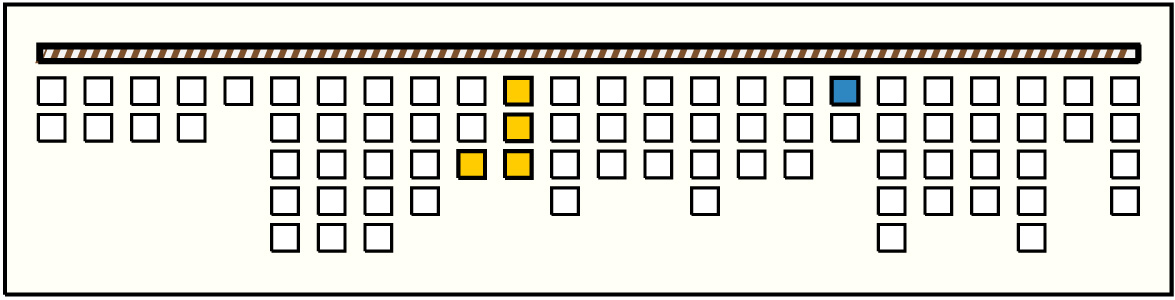p55_{18, 1} : 188_B-BB	188	4	p31: 6_B + p32: 72_AB + p33: 60_AB + p34: 50_AB
5	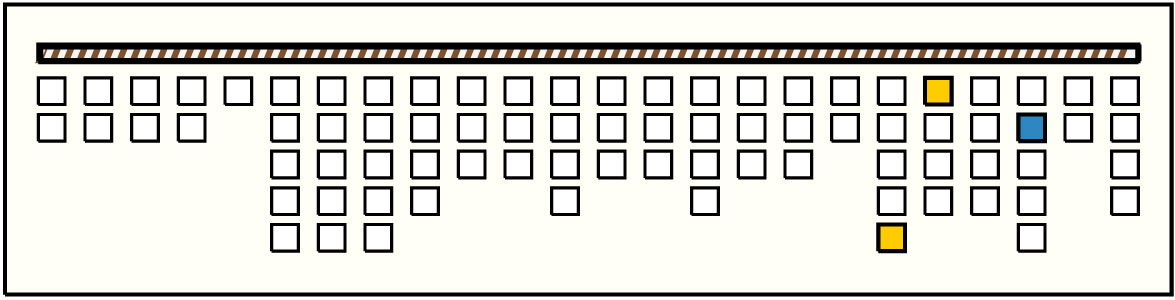p71_{22, 2} : 114_W-YG	114	2	p61: 106_AB-B + p62: 8_MB
6	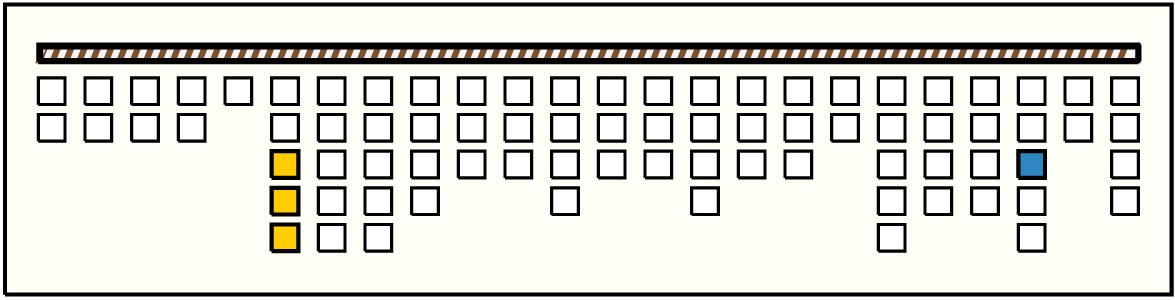p72_{22, 3} : 81_W-YG	81	3	p12: 5_B + p13: 4_W + p14: 72_W:B
7	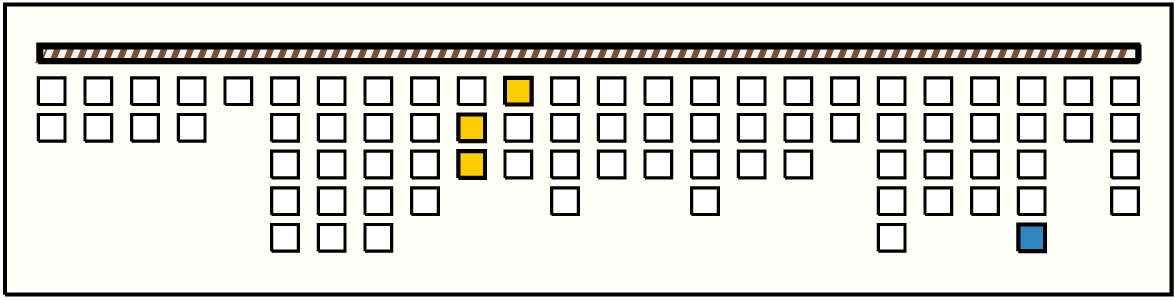p74_{22, 5} : 82_W-YG	82	3	p30: 4_B + p31: 6_B + p32: 72_AB
8	p80_{24, 4} : 28_AB	28	5	p75: 2_W:BB + p76: 0_B + p77: 0_W + p78: 0_W + p79: 26_AB

Khipu Notes:

Ascher Databook Notes:

This is one of several khipus acquired by the Museum in 1907 with provenance Ica. For a list of them, see UR1100.
By spacing and color patterning, the khipu is in 5 parts.
1. Part 1 is 4 groups of 2 pendants each and then 1 single pendant.
2. Part 2 is 3 groups of 5 pendants each. Each group has the same color pattern: B, YG:MP, YG/B, W, B:W. Subsidiaries on the first position are BB:W, and those on the second and fourth positions are B/MB/BB and B:W respectively.
3. Part 3 is 3 groups of 4, 3, and 3 pendants and then another 3 groups of 4, 3, and 3 pendants. In the first and fourth groups, the first pendants are the same color. Excluding these 2 cords, each of the 6 groups is unified by being one color. The values on the first pendants in the first and fourth groups are the sums of the rest of the values in their respective groups. Calling these 2 special pendants P310 and P340 (zero^th pendant in first and fourth groups of part 3):
  
  \[ P_{310} = \sum\limits_{j=1}^{3} P_{3ij}\;\;\;for\;i=(1,4) \]
4. Values in part 2 are the sums of values in part 3. The sums relate values in groups 1-3 of part 3 with values in corresponding positions in groups 4-6. In part 2, the sums appear in the group that corresponds to the summed positions. (For example, the sum of values in position 1 appears in group 1 and the sum of values in position 3 appears in group 3.) Specifically:
  
  P_2,i,2j-1 = P_3,j,i + P_3,j+3,i for j=(1,2,3) and i=(1,2,3)
5. Part 4 is 4 groups of 4,3,3,2 pendants respectively. The 3 or 4 pendant groups share a basic 4-color pattern: B-BB, B/HB, W, YG:MB. (Where there are only 3 pendants, it is the third position that is non-existent. ) Subsidiaries on position 1 are B-BB, and those on positions 2 and 4 are W/BB/B and B/YG respectively. The last 2-pendant group has the same first position color as the preceding groups.
6. Part 5 is 3 groups of 5, 4, and 4 pendants and then another 3 groups of 5, 2, and 4 pendants. As in part 3, the first pendants in the first and fourth groups are special pendants: they are the same color as each other; they are the same color as the 2 special pendants in part 3; they differ in color from the groups they are in; and their values are the sum of the other values in their respective groups. Thus:
  \[ P_{5i0} = \sum\limits_{j=1}^{4} P_{5ij}\;\;\;for\;i=(1,4) \]
7. The relationship of part 4 to part 5 is similar to the relationship of part 2 to part 3.
  
  P_4,i,j = P_5,j,i + P_5,j+3,i for j=(1,2) and i=(1,2,3,4)